时间序列预测基本概念

例如kaggle上的这两个比赛，都是带有时序性质，但形式上确实tabular data的形式的问题。

二者很多时候是可以直接做转化的。即我们可以把这类问题通过滑窗的方式转化为时间序列回归或时间序列分类的问题。

带有时序信息的tabular data的形式是每个item的每个time step都带有标签信息，对于item而言共有time step个标签，而纯粹的时序应用则是每个item的多个step只有1个标签信息，这是二者的数据形式上的区别。

时间序列分析：

类似于处理图数据或者是文本数据，时间序列有其专门的eda的方式，除了传统的无序的结构化数据之外，时间序列分析还需要分析序列数据的其它方面；时间序列分析提供了一系列技术，可以更好地理解数据集。 其中最有用的是将时间序列分解为4个组成部分：

1、base-level 序列的baseline值，是某个常数的定值。

2、趋势： 随时间变化的序列的变化模式，通常是线性的增加或减少行为。

3、季节性：我更喜欢称之为周期性，即序列数据随时间变化的重复模式或周期行为。

4、噪音：模型无法解释（拟合）的噪音

所有的时间序列数据都有一个level值，大部分时间序列数据都有噪声，并不是所有时间序列数据都有趋势性和周期性，时间序列数据的一个重要特征是时间上存在相互依赖性，即样本不是独立同分布的而是存在相关性的例如股票的数据，今天的股票价格可能受昨天的封板影响。

时间序列的这些特性是经典的时间序列方法的基础，例如ma、arima等经典的经济学模型（为了区分机器学习和深度学习方法，我们这里称之为经济学模型，因为金融专业的教材里专门涉及到这类问题）

实际的时间序列分析面临的问题：

在实际应用过程中，时间序列的分量往往是非常复杂的，这也是为什么业界的forecasting做的效果一直差强人意的主要原因，因为我们目前面临的很多时序应用的数据，除了上述的基本分量之外，还存在着例如：

1.节假日效应；

2.政治风险事件；

3.特殊的网络事件（流量预测相关尤其是）；

4.多周期多个趋势的混合构成；

。。。。

除此之外，在典型的例如金融领域，stock的价格预测常常更加复杂，因为可能存在很多的变量是无法观测的（例如舆情事件的获取涉及到爬虫和nlp，技术上是比较复杂的）或观测很复杂的。

建模前的目的要明确

在进行时序数据建模之前，进行预测时，明确建模的目的很重要。

1.拥有多少数据，并且如何将它们汇总在一起？更多的数据通常更有用，这为探索性数据分析，模型测试和调整以及模型稳定性、准确性等提供了更好的基础。

2.所需的预测时间跨度是多少？短期，中期还是长期？较短的时间范围通常更容易以较高的置信度进行预测，时间序列预测的周期越长，其预测的置信度越难以保证；

3.预测是否可以随时间推移而经常更新，或者必须进行一次建模并保持不变？当新信息可用时更新模型通常会得到更准确的预测模型。

4.需要什么时间频率？通常可以以较低或较高的频率进行预测，通常短周期的数据噪声较多，曲线较为坑坑洼洼，中场周期的数据噪声较少，曲线较为平滑，时间序列数据通常需要清理，缩放甚至转换。

例如：

1、频率：也许数据提供的频率太高而无法建模，或者由于时间间隔不均匀，需要重新采样才能用于某些模型。

2、离群值：可能存在需要识别和处理的时间序列异常。

3、缺失：可能存在需要插入或估算的缺失数据。通常，时间序列问题是实时的，不断为预测提供新的机会。这增加了时间序列预测的实时性，可以迅速弥补错误的假设，建模错误以及我们可能愚弄自己的所有其他方式。

时间序列预测的应用

1、根据患者的心电图序列数据判断患者的健康状态；

2、预测每天的股票收盘价。

3、预测城市中所有医院每年的出生率。

4、预测电商、商店每天售出的产品的销售量。

5、预测每天通过火车站的乘客数量。

6、预测每个季度的州失业情况。

7、预测每小时预测服务器上的利用率需求。

8、预测每个繁殖季节某个州的兔子数量。

9、预测一个城市每天的平均汽油价格。

。。。。。

时间序列问题的细分：

首先，时间序列问题可以划分为许多块：

1.forecasting；

2.时序回归和分类；

3.时序聚类；

4.时序异常检测

等等等等。

这里主要介绍forecasting部分。

forecasting分为单序列/多序列+单变量/多变量+单步/多步 时间序列预测，

其中，统计学模型，例如arima，holtwinters，fbprophet等等只能处理单序列问题，所谓单序列，即我们自始自终分析和预测的数据都是来自于同一个客观存在的事物，例如发电厂的电力预测，我们常常就是只对这一个发电厂的电力数据负责而不涉及到去处理其它电厂的序列数据。如果要处理多序列的问题，则使用统计学方法需要为每一个单序列单独训练一个模型，本质上还是做单序列的事情；

单变量时间序列预测问题，你只有标签，例如股票每天的收盘价，网页每天的流量，你所做的事情就是用历史的价格或者流量预测未来的价格或流量；

目前大部分互联网公司或量化基金公司处理的数据类型都不可能是单变量，基本上是多变量问题， 因为历史的数据只能为未来的洞见提供一小部分的见解 。

多变量时间序列预测，除了标签之外，你还有其它的特征，例如以股票的收盘价为例，你还有股票的换手率、股票对应的上市公司所属的行业等，这些额外的特征可以是序列相关的也可以是序列无关的，不过很多地方认为多变量时间序列预测中，额外的多个变量应该也是序列型数据，对此并不认同，例如股票的行业也可以按照时间做repeat转化为类似序列的数据形式来建模，常见的业务场景并不一定所有特征都是序列形式的。

除此之外，单变量和多变量时间序列预测又分别有两个更加细致的分类，即单步时间序列预测与多步时间序列预测，单步指你只需要预测未来一个时间单位的结果，例如你需要预测未来一天、一周、一个月的电商的某个商品的销量，但是注意，如果你预测的是未来一天，你的训练样本也要保证相同的时间维度，不能用以天为单位的样本预测未来一个周或者以周为单位预测未来一天；多步时间序列预测，顾名思义，就是预测未来多个时间单位的结果，例如以天为单位的训练样本，预测为了5天、10天。。。等多个时间单位的结果；

关于多步时间序列预测，比单步预测复杂得多，后面会详细描述。

如何处理时间序列预测问题？

转化为有监督的机器学习或深度学习问题：

最常见最直接也比较简单强大的一种做法，时间序列问题转化为有监督学习问题的核心在于：

1.特征工程：

实际上很简单，就是把时间序列数据的序列性通过特征工程的方式表征出来，因为传统的机器学习（lr，gbdt等）主要处理二维数据，对于时序这种三维数据往往无法直接建模，因此我们需要通过特征工程将时序的依赖性表达出来；

2.网络结构的设计：

对于传统的ml而言，核心在于特征工程，而对于dl而言，特征工程和网络结构的设计（超参数的各种调整）都是很重要的，dl在forecasting问题中的成果也是相当的多；

时间序列数据中的特征工程方法：

核心就是3个特征工程方法：

1、lag features；

2、时间窗函数；

3、滞后算子+时间窗函数

除此之外，还有一个常见的特征工程方法就是对日期进行展开，包括了：

1、一天中的小时，可以用于表示凌晨、上午、中午、下午、晚上、半夜

2、是否营业时间

3、是否周末。

4、是哪一个积极额

5、一年中的业务季度。

6、是否夏令时。

7、是否有公共假期，例如国庆、劳动节等，对于电商时序预测来说，双十一、六一八等是非常重要的节日；

8、是否是闰年

。。。。。 基本上pandas的时间函数可以囊括大部分功能了

举个例子就能说清楚了，下面我们分四种类型问题来说明：

1、单变量单步：

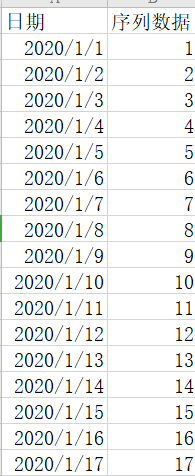
上图是典型的单变量时间序列预测问题，假设我们要预测1-18号的序列数据是多少，首先，加入长度为1day的滞后算子：

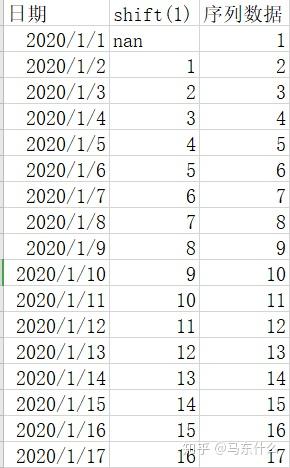
可以看到，这样就转化为我们熟悉的回归问题了，特征是标签的shift(1)变换（pandas的shift函数可以直接处理），这样问题就转化为“用昨天的序列数据来预测今天的序列数据”，当然也可以加入更多的shift操作例如：

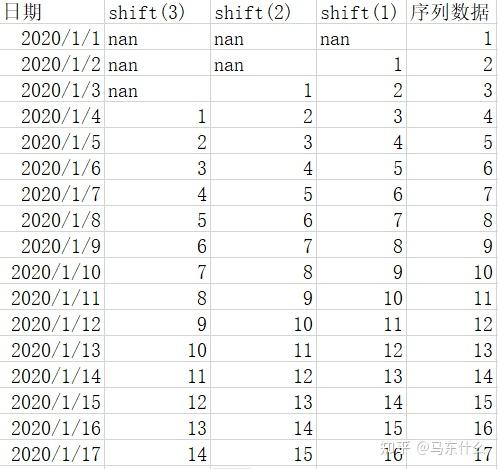
这样问题就变成了“用过去三天的序列数据来预测今天的序列数据”

因此，通过滞后算子我们可以很简单的将序列问题转化为有监督学习中的回归问题，假设业务的需要是提前三天预测，则我们只需要去掉shift(2)和shift(1)就可以了；

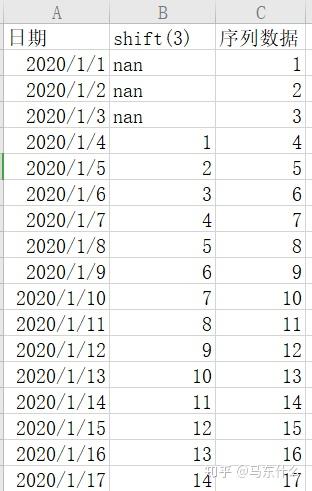
当然了，如果业务需求如上，我们可以加入shift4，shift5.。。shiftn的滞后数据来构建有监督回归模型，具体取多少个shift，根据实际的问题和效果以及业务经验来定了；

上面介绍了滞后算子，下面介绍时间窗 ，其实原理也很简单，和风控里常用的时间窗概念是一样的，还是以上面的问题为例，我们可以通过pandas的rolling或者expand来计算过去XX天的的时间段内的标签的均值、标准差、方差、最大、最小、中位数、求和等，例如：

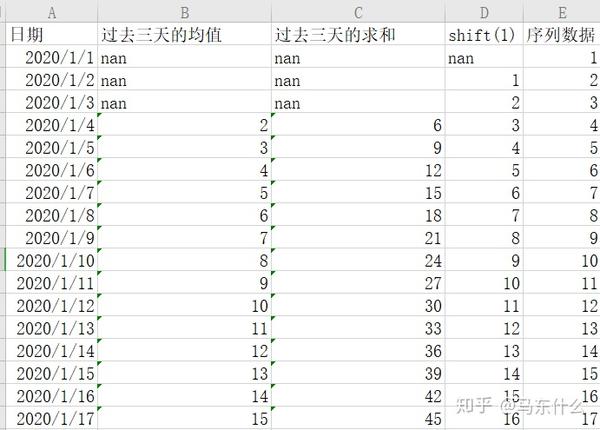
开源的时间序列处理的python library，比如tsfresh、scikit-time，darts等等所包含的重要概念都有时间窗函数，不过说老实话，真的懒得去看框架的api，一方面源码看起来费劲，如果不知道他内部怎么处理的用起来心有点慌，一方面感觉pandas能实现很多东西就不搞了。。。

滞后算子+时间窗 很好理解了，就是你特征工程算的是多少天前的某个时间段的统计指标，比如滞后算子是3，时间窗为7，则计算的是当前时间点往前推3天，到达了A时间点，然后A时间点再往前推七天来计算sum mean之类的，通过pandas的shift+rolling的方式很容易实现的；

2、单变量多步：

单变量多步的做法大体雷同，但是需要注意一些重要的细节问题：

还是以上面的例子为例，假设我们要预测未来三天的序列数据：

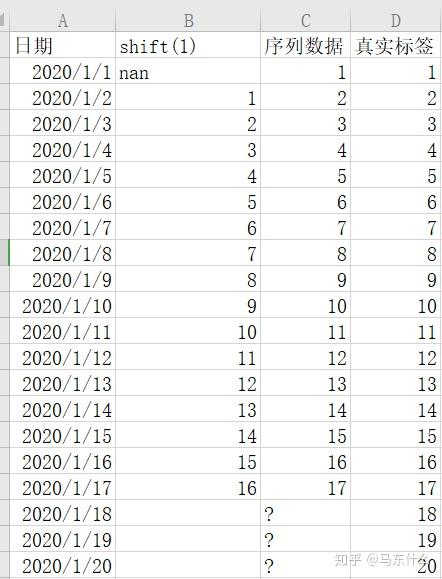
这个时候我们的滞后算子就不能用shift(1)也就是一天的滞后了，因为实际预测的时候，我们需要提前三天进行预测，也就是我们站在2020-01-17这一天，要预测未来三天的序列数据，这个时候，我们仅仅直到1-18号的前一天，也就是今天的序列数据是17，但是不可能知道19和20号的前一天的值是多少，因此，面对多步预测的时候，滞后算子是有一个上限的，例如这里预测未来三天，则我们的shift至少要从3开始取，

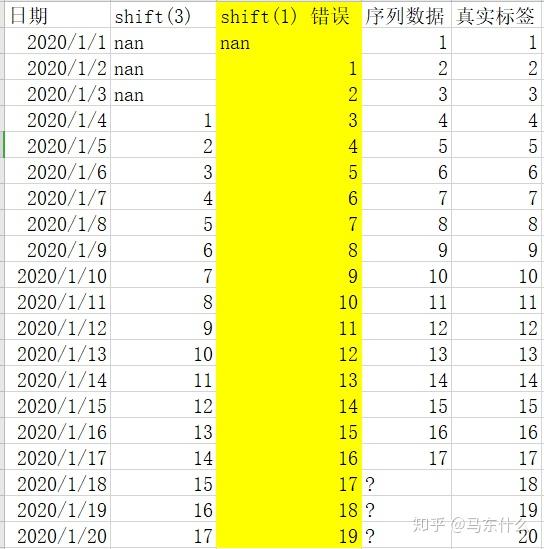
时间窗以及滞后算子+时间窗的思路也是一样的，不赘述；

上面是多步时间序列预测最简单的处理方法，通过放大滞后算子的窗口来构造特征，最终的形式还是转化为常规的回归问题来处理，我们可以用线性回归、xgb之类的常用算法来处理这个问题莫得问题，除此之外还有两种思路：

1、把多步预测转化为多个单步预测：

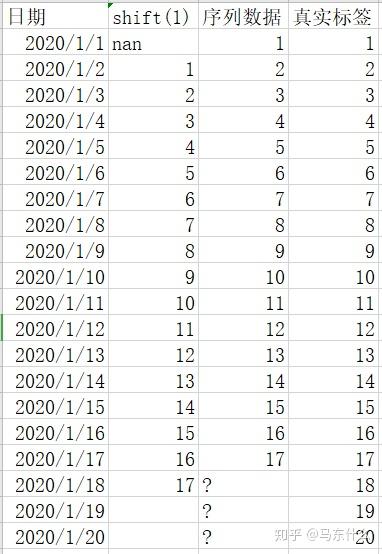
处理方法和单步预测一样，比如我们这里要预测未来三天，则我们按照预测未来一天来建模，当我们预测出1-18号的结果之后，假设预测结果为17.8，则我们可以将17.8作为1-19号的特征：

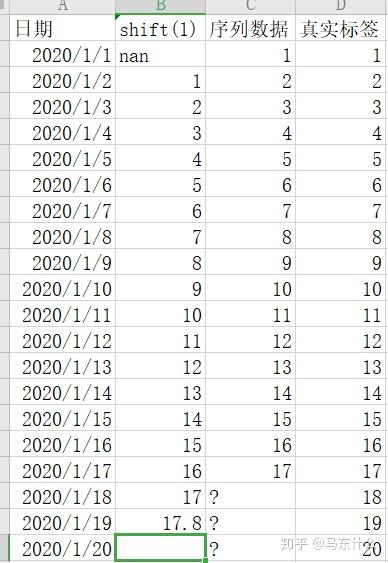
依次类推；

2、将多步预测转化为单步预测问题，局限性较大：

我们要预测未来三天，没问题，我们把未来三天直接转化为一个样本，表示 18 19 20三天的序列数据之和，然后样本也进行转换，（1、2、3），（2，3，4），（3，4，5）。。。（15，16，17），到此为止，我们将原始的数据转化为以3days为一个时间周期，这样问题又变成了单步时间序列预测了，不过这样方法局限性比较大，假设业务需求是要预测每一天的，这种方法就行不通；

前面提到的多步预测都是按照单标签回归的思路来建模的，复杂一点的，转化为多标签回归问题，对于多标签问题，目前常见的算法还是使用nn的灵活结构来构造，转化为一个多输出的问题：

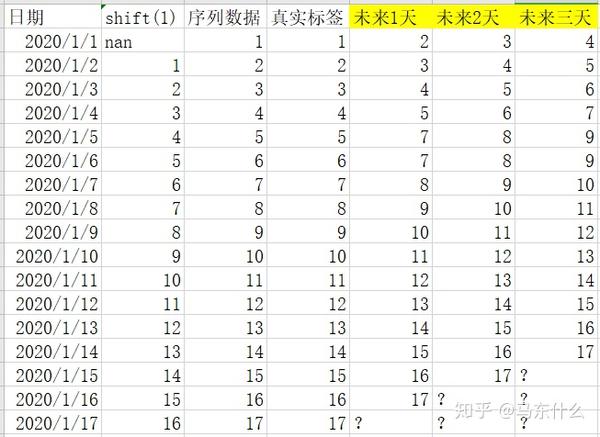
这种形式的数据，用lr或者gbdt之类的直接建模也可以，就是将多标签转化为多个单标签，我们可以针对未来一天先建模得到模型1，模型1的预测结果作为新的特征然后预测未来2天。。。就是前面我们提到的多步转单步的思路，还可以预测未来一天后，以预测的结果作为特征，构建一个未来两天的模型2.。。。。依此类推，然后构建，

如果使用nn的话，除了上述的这种方法，nn有自己特殊的建模方法直接进行多步预测，例如典型的LSTM，我们可以：

1、使用lstm的结构，不过这个lstm是多个输入对应多个输出的结构（比如过去7天预测未来3天），即MvN的结构；

2、使用seq2seq的结构（kaggle的web traffic比赛的top solution的方案，没看过具体的代码就知道用的这个方法）

ps：实际上这里的多标签回归的描述还需要补充一点就是，时序问题转化为多标签回归，多个标签之间还是有时序的依赖关系的，这种情况下用rnn特别合适。

下面介绍多变量的时间序列预测问题，同样：

多变量单步与多步：

前面已经介绍了单变量单步和多步了，后面多变量的就放在一起介绍吧：

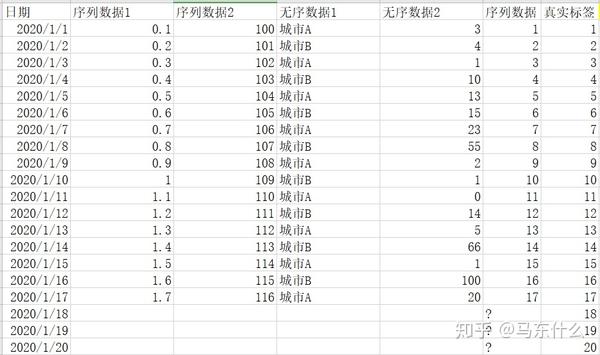
多变量单步预测相对于单变量单步差不太多，只不过多了更多的特征，一般来说，多出来的特征可以是有序的也可以是无序的例如典型的电商销量预测问题，特征可以是一些序列数据也可以是城市这样的无序数据，做法一样的，对于无序特征来说，我们也可以使用滞后算子和时间窗函数，对于有序特征更可以了，其它的思路就和单步差不多了：

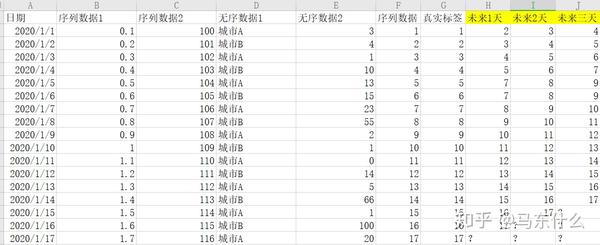
同样，也可以我们上面提到的nn的结构来进行预测；

时间序列问题的特点在于，针对于同一个业务问题，我们可以转化成不同类型的时间序列预测问题来求解，以电商的销量预测为例，我们可以仅使用序列数据，结合arima、propeht这类模型来建模，也可以通过滞后算子和时间窗来构造有监督学习问题，多步可能可以转单步，单步也可能可以转多步预测，非常灵活；

除此之外，还有其它的一些问题形式，业务中和比赛中遇到的问题会更加复杂：

1、多序列数据，我们前面所说到的四种问题类型实际上都是单序列数据，以电商预测为例，假设我们要预测上海市的某个电商产品A的销量，则问题是单序列问题，形式大概是这样的：

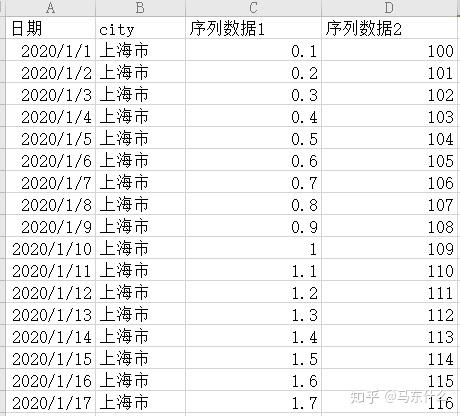
但是假设这个电商在全国一共50个城市都有产品A的业务，则实际上我们一共有50个序列数据，即多序列问题，这种问题，比较naive的做法就是针对每个城市构建一个时序模型，则我们一共要构建50个时序模型，但是实际上这种方法往往行不通，因为很多中小城市的序列数据少的可怜，根本没有办法用于建模，这个时候我们的思路实际上是讲所有的城市的序列数据按照 city进行合并，变成一个大矩阵，然后转化为有监督学习问题来求解，城市作为一个特征city入模，形式大概是这样：

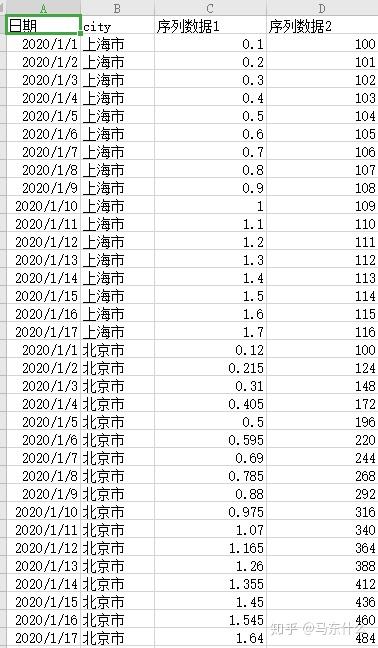
当然，针对于单序列问题的算法比如arima、fbpropeht之类的可以作为benchmark，也可以作为上述有监督模型的特征提取工具进行特征提取等；

2、带有序列特征的常规问题：

这种也很常见，例如 整体的无序数据中存在一些序列数据，典型的，风控中，同一个用户的多条样本记录，例如借贷信息是按照时间排列的，常见的处理方法基本就是时间窗函数处理，实际上和第一种形式是类似的；

3、其它的有待补充，可能也许大概应该还有别的类型

示例代码

下面我们就以一段demo代码来学习一下时间序列预测问题的解法：

import pandas as pd
from pandas import read_csv
from pandas import DataFrame
series = read_csv('daily-minimum-temperatures-in-me.csv')
series.Date=pd.to_datetime(series.Date)
series.index=series.Date

我们选择墨西哥温度数据来作为demo数据

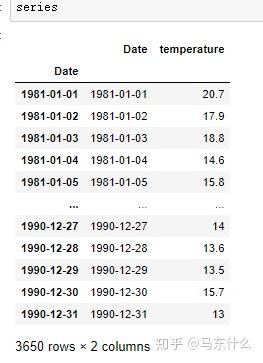
首先，做日期的展开：

dataframe = DataFrame()
dataframe['month'] = [series.index[i].month for i in range(len(series))]
dataframe['day'] = [series.index[i].day for i in range(len(series))]
dataframe['temperatute']=series.temperature.values
print(dataframe.head(5))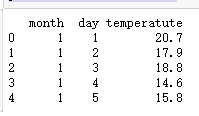

这里简单做了month和day的日期提取，基本上pandas可以一套搞定前面提到过的所有的日期展开的特征衍生方法；

然后是lag特征即滞后算子

temps = DataFrame(dataframe.temperatute.values)
dataframe = pd.concat([temps.shift(1), temps], axis=1)
dataframe.columns = ['t', 't+1']
print(dataframe.head(5))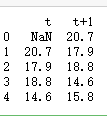

dataframe = pd.concat([temps.shift(3), temps.shift(2), temps.shift(1), temps], axis=1)
dataframe.columns = ['t-2', 't-1', 't', 't+1']
print(dataframe.head(5))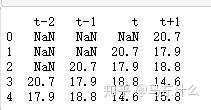

就是如此的easy~~,可以做一个简单的封装

def series_to_supervised(data, n_in=1, n_out=1, dropnan=False,col='label1'): #label1表示你的序列的特征对应的col的名字
    data=data[col].values.tolist()
    n_vars = 1 if type(data) is list else data.shape[1]
    df = pd.DataFrame(data)
    cols, names = [], []
    # i: n_in, n_in-1, ..., 1
    # 代表t-n_in, ... ,t-1
    for i in range(n_in, 0, -1):
        cols.append(df.shift(i))
        names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)]
    for i in range(0, n_out):
        cols.append(df.shift(-i))
        if i == 0:
            names += [('var%d(t)' % (j+1)) for j in range(n_vars)]
        else:
            names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)]
    agg = pd.concat(cols, axis=1)
    agg.columns = names
    if dropnan:
        agg.dropna(inplace=True)
    return agg
series_to_supervised(temps,5,1,False,col=0)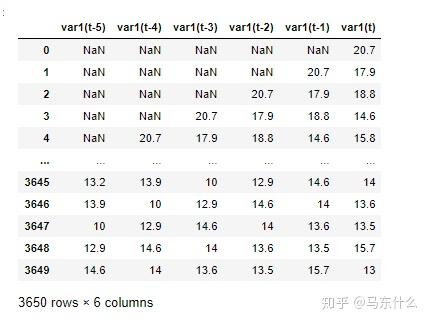

其中var1(t)就是我们原始的要预测的序列数据

最后是时间窗函数，所谓时间窗函数其实就是统计每一个序列的时间点的历史的某一段时间窗口的时间内的序列数据的各种统计指标，常见的包括mean max min sum std等等

temps.replace('?0.2','0.2',inplace=True)
temps.replace('?0.8','0.8',inplace=True)
temps.replace('?0.1','0.1',inplace=True)
temps = DataFrame(series.temperature.values).astype(float)
width = 3
shifted = temps.shift(width - 1)
window = shifted.rolling(window=width)
dataframe = pd.concat([window.min(), window.mean(), window.max(), temps], axis=1)
dataframe.columns = ['min', 'mean', 'max', 't+1']
print(dataframe.head(5))

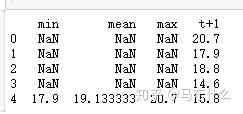
除了rolling之外，pandas还有一个expanding的方法也很好用
window = temps.expanding()
dataframe = pd.concat([window.min(), window.mean(), window.max(), temps.shift(-1)], axis=1)
dataframe.columns = ['min', 'mean', 'max', 't+1']
print(dataframe.head(5))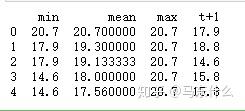

下面我们通过一个简单的事例来熟悉下pandas的rolling和expanding

import pandas as pd
import numpy as np
df=pd.DataFrame([1,2,3,5],columns=['a'])
print(df)
print(df.rolling(3,min_periods=2).sum())
print(df.rolling(4,min_periods=2,center=True).sum())

这里min_periods用于表示当我们的数据不足一个时间窗的时候，最小的可计算的数据长度

expanding是没有固定窗口概念的，实际上可以将expanding看出是累计计算，例如sum，是分别对1~4的窗口的累计计算。

时间序列数据的可视化：

可视化在时间序列分析和预测中起着重要作用。 原始样本数据的图表可以提供有价值的信息，帮助识别时间结构，例如趋势，周期，和季节性，这终将会影响模型的选择。 一个问题是，在时间序列预测领域中的许多新手都无法使用线图。 在本教程中，我们将介绍您可以在自己的时间序列数据上使用的6种不同类型的可视化。 他们是：

1.线图。

2.直方图和密度图。

3.箱形图和晶须图。

4.热图。

5.滞后图或散点图。

6.自相关图。

重点放在单变量时间序列上，当每个时间步长有多个观察值时，这些技术同样适用于多元时间序列。

from pandas import read_csv
from matplotlib import pyplot
temps.columns=['temperature']
temps.plot()
pyplot.show()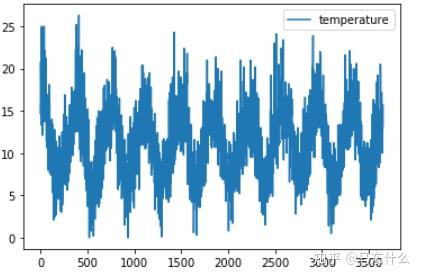

temps.plot(style='k.')
pyplot.show()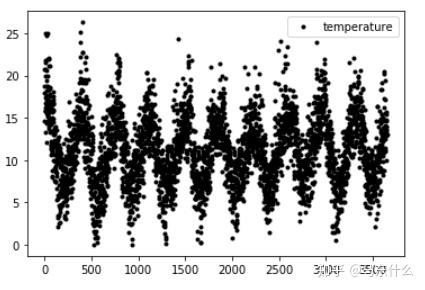

通过线图我们可以较好的看出数据整体的分布情况以及其大致的规律性；

from pandas import Grouper
temps.index=series.index
groups = temps.groupby(Grouper(freq='A'))
years = DataFrame()
for name, group in groups:
    years[name.year] = group.temperature.values
years.plot(subplots=True, legend=False,figsize=(15,15))
pyplot.show()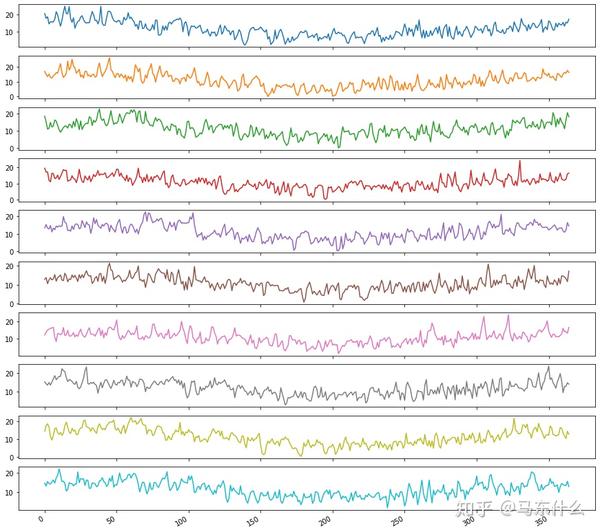

我们可以按年对数据进行分别的可视化，这样可以很好的看出时间的年周期性，可以看到每年的数据走势基本上相差无几，如果要看月的话就按照月聚合，以此类推；

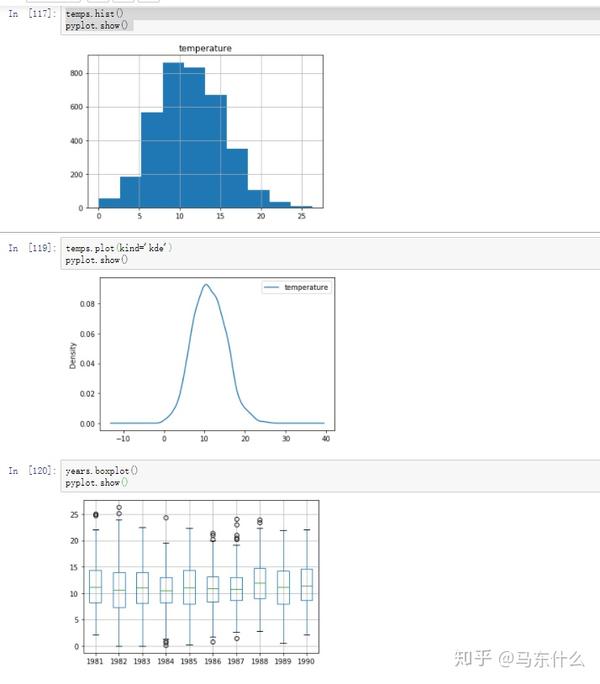
通过上述的hist kde以及箱型图我们可以很好的比较不同年份的序列数据的差异和相似性以及，通过箱型图，我们可以很好的看出时间序列中的异常点（outliers）；

groups = temps.groupby(Grouper(freq='A'))
years = DataFrame()
for name, group in groups:
    years[name.year] = group.temperature.values
years = years.T
pyplot.matshow(years, interpolation=None, aspect='auto')
pyplot.show()

通过heatmap图我们可以很好的看出数据的变化趋势；

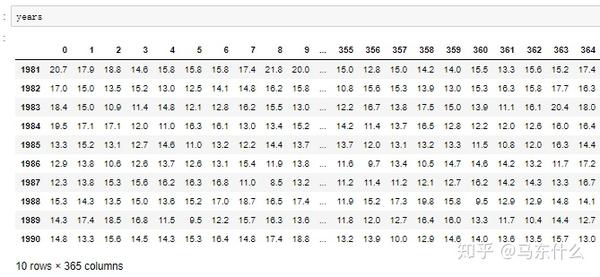
上图是按照天展开的，我们也可以按照月来展开；

one_year = series['1990']
groups = one_year.groupby(Grouper(freq='M'))
months = pd.concat([DataFrame(x[1].values) for x in groups], axis=1)
months = DataFrame(months)
months.columns = list(range(1,25))
months=months[list(range(2,25,2))].astype(float).fillna(months.mean())
pyplot.matshow(months, interpolation=None, aspect='auto')
pyplot.show()

我们取1990年的数据，然后按照月份展开：

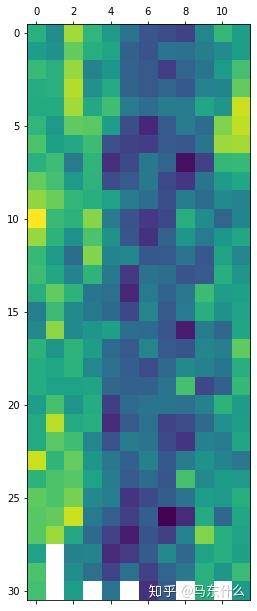
这里可以更加细致的看出每个月以及每个月的每一天的序列数据变化情况

for lag in [1,2,3,4,5,6,7,8,9,10]:
    pyplot.figure(figsize=(5,5))
    lag_plot(temps.temperature)
    pyplot.show()

滞后图

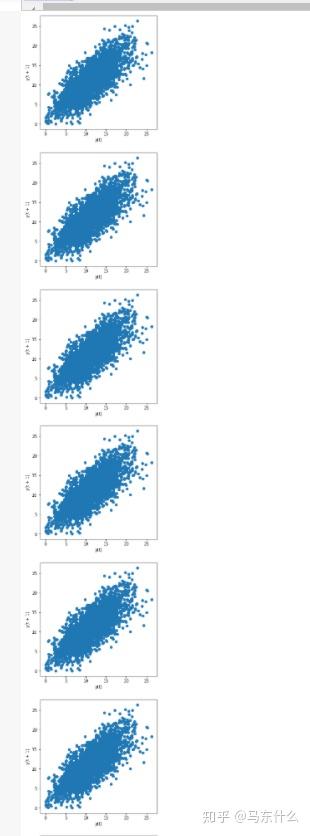
通过滞后图我们可以非常方便的看出不同的滞后时间数据与原始数据之间的整体的相关性情况；

自相关图

from pandas.plotting import autocorrelation_plot
autocorrelation_plot(temps.temperature)
pyplot.show()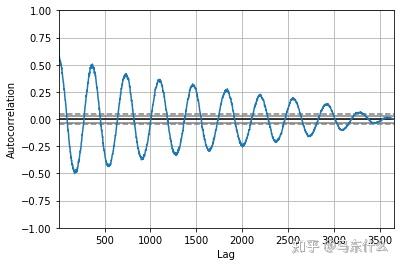

我们可以看到，对于上述的数据集，我们看到了强烈的负相关和正相关的循环。 上图捕获了某一个观测值与一年中相同和相反季节的观测值或过去时间的观测值之间的关系。 如本例中所示的正弦波是数据集中季节性的强烈信号。

补充： 自相关（英语：Autocorrelation），也叫序列相关，是一个信号于其自身在不同时间点的互相关。非正式地来说，它就是两次观察之间的相似度对它们之间的时间差的函数。它是找出重复模式（如被噪声掩盖的周期信号），或识别隐含在信号谐波频率中消失的基频的数学工具。自相关函数在不同的领域，定义不完全等效。在某些领域，自相关函数等同于自协方差。 由于时间序列的相关性与之前的相同系列的值进行了计算，这被称为序列相关或自相关。一个时间序列的自相关系数被称为自相关函数，或简称ACF。这个图被称为相关图或自相关图。 pandas的自相关图对相关系数没有做绝对值变换而statsmodels做了，上图也很简单，横轴代表了lag滞后的时间单位，例如上图种lag=500的时候，其实就是对原始的序列数据取shift(500)然后在对二者进行相关系数的计算得到的结果即为纵轴的坐标，通过自相关图我们可以很方便的看出序列数据的规律性。

import statsmodels.api as sm
sm.graphics.tsa.plot_acf(temps.temperature)
pyplot.figure(figsize=(12, 6))
pyplot.show()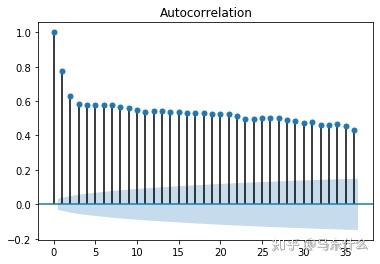

通过自相关图我们可以很容易看出不同周期的滞后算子与预测目标的关系，可以作为构造滞后特征的指导，例如上图滞后周期为1和2个单位的滞后数据与原始特征之间高相关我们可以选择做构造lag为1和2的特征。

重采样和插值：

时间序列问题中的采样和不均衡学习中涉及到的采样是不同的概念，时间序列中的采样实际上是对观测的时间粒度的放缩，例如：

1、上采样：增加采样频率的位置，例如从几分钟转化到到几秒钟（当然，你的数据本来得至少是秒级别的）。

2、下采样：减少采样频率的位置，例如从几天到几个月。

使用到重采样的场景有：

1、如果无法以想要进行预测的频率获得数据，则可能需要重新采样；

2、细粒度的时间周期误差太大则可以考虑聚合成更粗粒度的时间周期，从而将问题进行转换；

3、特征工程，重采样之后可以进行更多的特征衍生，例如日变成月，则可以提取关于月的一些衍生特征；

一个具体的例子，你有日的数据，但是需要你预测周的销量（例如双十一周），此时我们可以选择以天为单位预测双十一的销量再进行求和，也可以将天数据进行聚合转化为周，直接计算周的总销量；

当然，pandas的重采样函数可以非常方便的补足日期的缺失：

from pandas import read_csv
series = read_csv('sales-of-shampoo.csv')
series.index=pd.to_datetime(series.Month)
series.drop('Month',axis=1,inplace=True)
series.index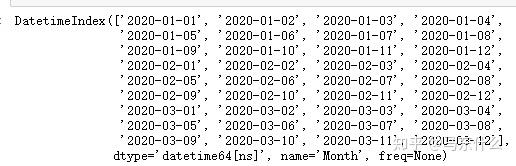

可以看到，上述的日期是有断层的，1-12号之后的数据没有了，为了日期上的连续性我们可以进行resample的操作来补足日期：

upsampled = series.resample('D').sum()
upsampled.head(72)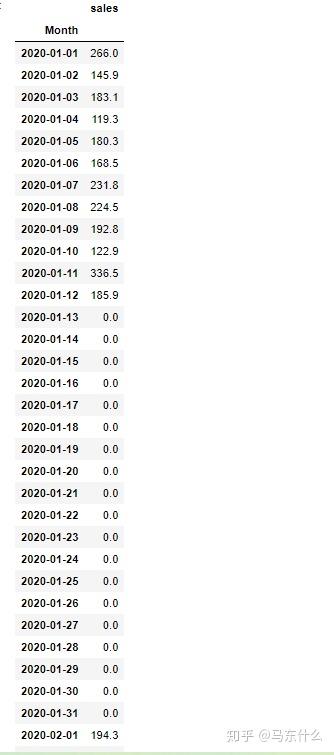

可以看到，这样我们就非常方便的对日期进行了补足；

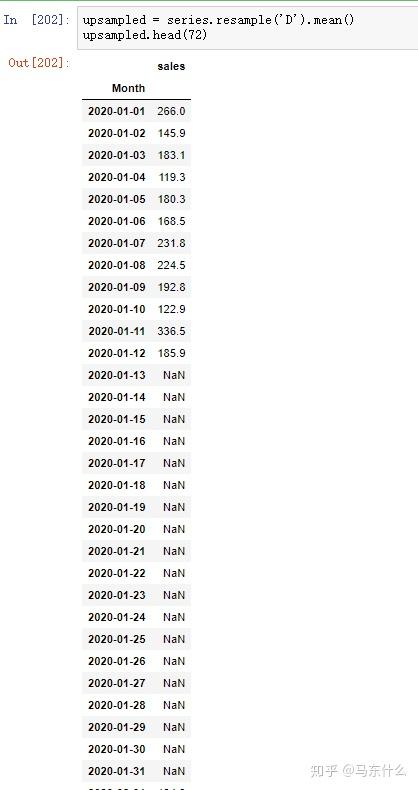
根据sum或者mean等算子的不同，缺失日期的补充策略也不同；

需要注意的是，如果要进行日期的补足，我们要把日期的特征变成index并且转化为time格式的才可以，否则会报错；

对于序列数据的插补，pandas的interpolate模块非常的方便：

data Frame.interpolate ( method='linear' , axis=0 , limit=None , inplace=False , limit_direction=None , limit_area=None , downcast=None , **kwargs )

method包括了：

• ‘linear’：忽略索引，并将值等距地对待。这是MultiIndexes支持的唯一方法。

这种插补的思路很简单，就是等距插补，如下的例子：

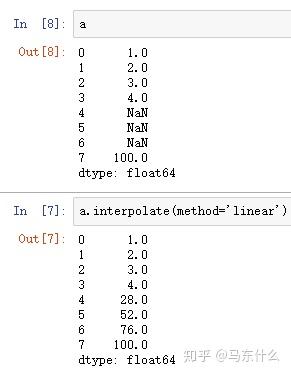
（100-4）/4=24，第一个插补值 4+24=28，第二个 26+24=52.。。。。

• ‘time’：处理每日和更高分辨率的数据以内插给定的时间间隔长度。

time和linear的原理基本一样，只不过time可以根据datetimeindex来进行线性插补

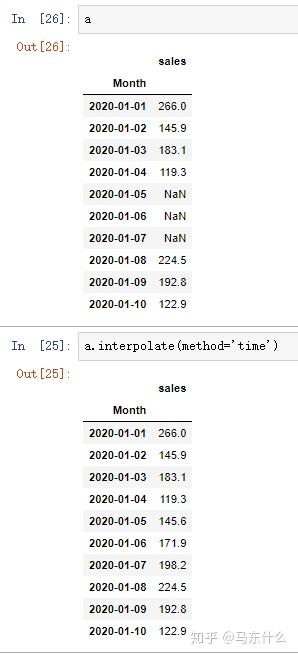
见上，注意，index必须是datetime类型的日期数据

• ‘index’，‘values’：使用索引的实际数值。

很奇怪，index和values的结果和linear完全一样：

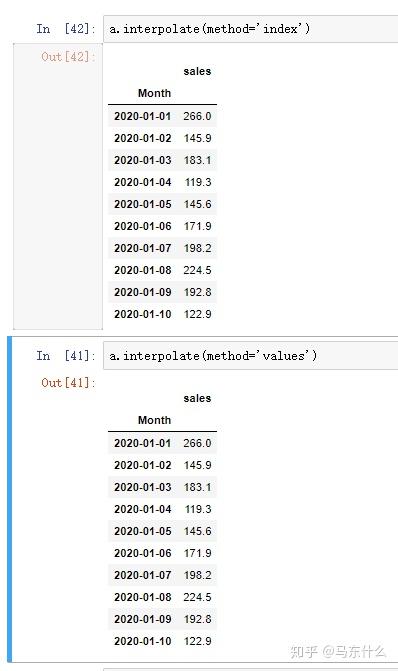
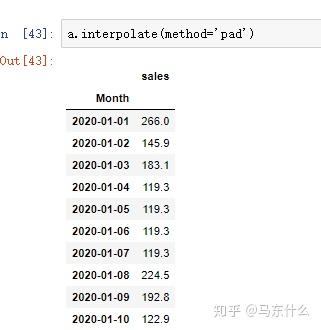
• ‘pad’：使用现有值填写NaN。

pad只能支持limit_direction='forward'的形式，因此只是用第一个缺失值前面的那个数来直接填充：

• ‘nearest’，

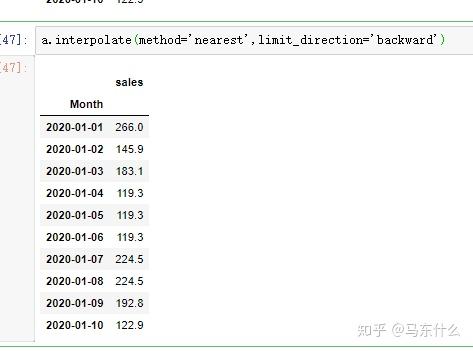
顾名思义，取最近的那个数值直接进行赋值，可以是前向后向或者双向，通过limit_direction来设置

• ‘zero’，‘slinear’，‘quadratic’，‘cubic’，‘spline’，‘barycentric’，‘polynomial’：传递给scipy.interpolate.interp1d。这些方法使用索引的数值。 ‘polynomial’和‘spline’都要求您还指定一个order(int)，例如 df.interpolate(method='polynomial', order=5) 。
• ‘krogh’，‘piecewise_polynomial’，‘spline’，‘pchip’，‘akima’：环绕具有相似名称的SciPy插值方法。看到Notes。
• ‘from_derivatives’：参考scipy.interpolate.BPoly.from_derivatives它替换了scipy 0.18中的‘piecewise_polynomial’插值方法。

limit：要填充的连续NaN的最大数量。必须大于0，不设置则默认填充所有nan

limit_direction： {‘forward’, ‘backward’, ‘both’}, 默认为 ‘forward’

如果指定了限制，则将沿该方向填充连续的NaN，就是前向、后向、双向填充的意思；

limit_area： {None, ‘inside’, ‘outside’}, 默认为 None

如果指定了限制，则连续的NaN将填充此限制。

• None ：无填充限制
• ‘inside’：仅填充有效值(内插)包围的NaN。
• ‘outside’：仅将NaN填充到有效值之外(外推)。

除此之外，时间序列数据的插补也可以做的非常复杂，下面这个github的仓库总结的很全呢：

时序序列预测中的数据转换

数据转换

数据变换旨在消除噪声并改善时间序列预测中的信号。对于给定的预测问题，很难选择好的甚至最佳的变换。有很多变换可供选择，每个变换都有不同的功能，对于问题的影响要实际测试了才知道：

from pandas import read_csv
from matplotlib import pyplot
series = read_csv('airline-passengers.csv')
pyplot.figure(1)
# line plot
pyplot.subplot(211)
pyplot.plot(series.passengers)
# histogram
pyplot.subplot(212)
pyplot.hist(series.passengers)
pyplot.show()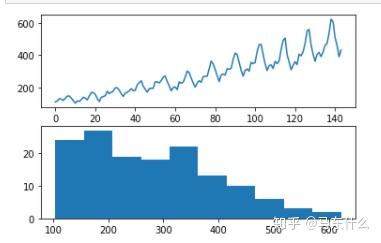

可以看到，上述的数据集是不稳定的，因为显然可以看出，观测值的均值和方差会时间变化。 这使得很难使用ARIMA等经典统计方法和神经网络等更复杂的机器学习方法进行建模。

（补充，首先，经典的时序模型如arima需要时间序列是平稳的，平稳的时间序列的均值和方差是不随时间变换的，然后是机器学习方法，机器学习或者深度学习的本质假设是iid，即独立同分布，显然，均值和方差随着时间变化意味着数据都是不独立同分布的；）

观察上述似乎既有趋势增长又是季节性因素造成的。

下面介绍第一种变换， 平方根变换：

from matplotlib import pyplot
series = [i**2 for i in range(1,100)]
pyplot.figure(1)
# line plot
pyplot.subplot(211)
pyplot.plot(series)
# histogram
pyplot.subplot(212)
pyplot.hist(series)
pyplot.show()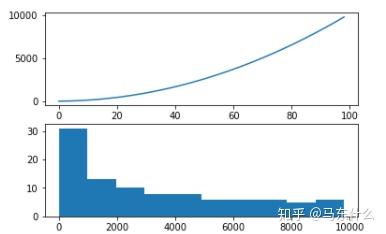

如果在时间序列数据中看到这样的结构，则序列数据可能是二次增长趋势。 可以通过平方运算的逆运算（平方根）将其删除或线性化。 因为该示例是完美的二次方，所以我们希望转换后的数据的线图显示一条直线。

from matplotlib import pyplot
from numpy import sqrt
series = [i**2 for i in range(1,100)]
# sqrt transform
transform = series = sqrt(series)
pyplot.figure(1)
# line plot
pyplot.subplot(211)
pyplot.plot(transform)
# histogram
pyplot.subplot(212)
pyplot.hist(transform)
pyplot.show()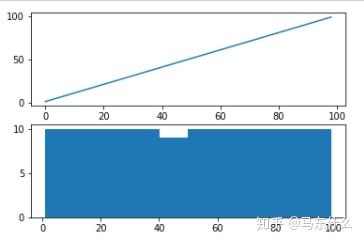

我们可以看到，正如预期的那样，二次趋势在进行平方根转化年之后呈线性；

我们在查看一个航空的旅客数据：航空公司乘客数据集有可能显示二次方增长。 如果是这种情况，那么我们可以期望平方根变换将增长趋势降低为线性，并将观测值的分布更改为近似高斯分布。 下面的示例执行数据集的平方根并绘制结果。

dataframe=series.copy(deep=True)
dataframe['passengers'] = np.sqrt(dataframe['passengers'].values)
pyplot.figure(1)
# line plot
pyplot.subplot(211)
pyplot.plot(dataframe['passengers'])
# histogram
pyplot.subplot(212)
pyplot.hist(dataframe['passengers'])
pyplot.show()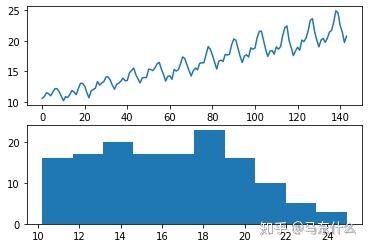

我们可以看到趋势有所减少，但并未消除。 折线图仍然显示每个周期之间的变化越来越大。 直方图仍然在分布的右侧显示一条长尾巴，表明呈指数分布或长尾分布。

然后介绍一下对数变换：

对数变换

一类更为极端的数据的趋势是指数型的， 通过取值的对数，可以使具有指数分布的时间序列转换为线性，这称为对数变换。 与上面的平方和平方根的情况一样，我们可以用一个简单的例子来证明这一点。

from matplotlib import pyplot
from math import exp
series = [exp(i) for i in range(1,100)]
pyplot.figure(1)
# line plot
pyplot.subplot(211)
pyplot.plot(series)
# histogram
pyplot.subplot(212)
pyplot.hist(series)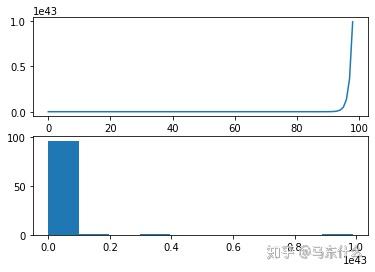

运行示例将创建该系列的折线图和观测值分布的直方图。 我们在折线图上看到一个极端的增加，在直方图上看到一个同样极端的长尾分布。同样，我们可以通过取值的自然对数将这个数据转化为线性。 这将使数据的分布均匀：

from matplotlib import pyplot
from math import exp
from numpy import log
series = [exp(i) for i in range(1,100)]
transform = log(series)
pyplot.figure(1)
# line plot
pyplot.subplot(211)
pyplot.plot(transform)
# histogram
pyplot.subplot(212)
pyplot.hist(transform)
pyplot.show()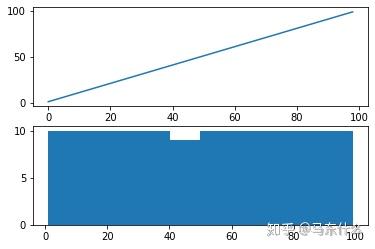

同样，我们对航空数据也进行对数变换看看结果如何：

from pandas import DataFrame
series = read_csv('airline-passengers.csv')
dataframe = DataFrame(series.passengers.values)
dataframe.columns = ['passengers']
dataframe['passengers'] = log(dataframe['passengers'])
pyplot.figure(1)
# line plot
pyplot.subplot(211)
pyplot.plot(dataframe['passengers'])
# histogram
pyplot.subplot(212)
pyplot.hist(dataframe['passengers'])
pyplot.show()

对数变换在时间序列数据中很受欢迎，因为它们可以有效消除指数方差。 重要的是要注意，此操作假设值是正数且非零。通常通过添加固定常数来变换观测值以确保所有输入值均满足此要求。 例如：

transform = log(constant + x)

其中log是自然对数，transform是变换后的序列，常数是将所有观测值提升到零以上的固定值，x是时间序列。

一般常见的方法，constant取得是原始数据的最小负数值-1；

其它的一些转换方法

首先介绍的是boxcox变换：

平方根变换和对数变换属于一类称为幂变换的变换。 Box-Cox是二者的泛化形式，它 是一种可配置的数据转换方法，它支持平方根和对数转换，以及其它相关转换。

先来看一下怎么用：

from pandas import DataFrame
from scipy.stats import boxcox
series = read_csv('airline-passengers.csv')
dataframe = DataFrame(series.passengers.values)
dataframe.columns = ['passengers']
dataframe['passengers'] = boxcox(dataframe['passengers'], lmbda=0.0)
pyplot.figure(1)
# line plot
pyplot.subplot(211)
pyplot.plot(dataframe['passengers'])
# histogram
pyplot.subplot(212)
pyplot.hist(dataframe['passengers'])
pyplot.show()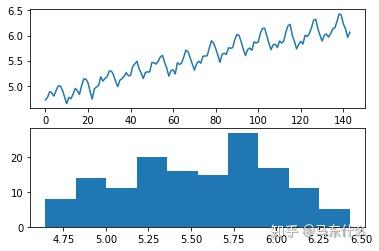

我们可以将lambda参数设置为None（默认值），然后让该函数找到经过统计调整的值。 下面的示例演示了此用法，同时返回转换后的数据集和所选的lambda值。

from pandas import DataFrame
from scipy.stats import boxcox
series = read_csv('airline-passengers.csv')
dataframe = DataFrame(series.passengers.values)
dataframe.columns = ['passengers']
dataframe['passengers'], lam = boxcox(dataframe['passengers'])
print('Lambda: %f' % lam)
pyplot.figure(1)
# line plot
pyplot.subplot(211)
pyplot.plot(dataframe['passengers'])
# histogram
pyplot.subplot(212)
pyplot.hist(dataframe['passengers'])
pyplot.show()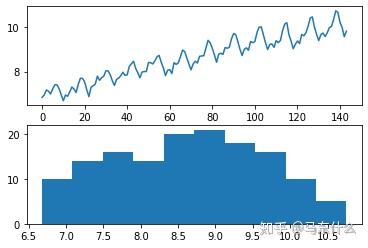

运行示例将发现lambda值为0.148023。 我们可以看到，它非常接近lambda值0.0，从而类似于对数变换，但又不是对数变换，程度更深一些。

补充：boxcox变换：

Box-Cox变换是Box和Cox在1964年提出的一种广义幂变换方法，是统计建模中常用的一种 数据 变换，用于连续的响应变量不满足正态分布的情况。Box-Cox变换之后，可以一定程度上减小不可观测的误差和预测变量的相关性。Box-Cox变换的主要特点是引入一个参数，通过数据本身估计该参数进而确定应采取的数据变换形式，Box-Cox变换可以明显地改善数据的正态性、对称性和方差相等性，对许多实际数据都是行之有效的

那么当我们使用scipy的boxcox的时候，不指定lambda，scipy是如何确定lambda值的？

实际上即使通过极大似然法推导的，因为我们是假设boxcox转换之后，变量能够服从正态分布，所以可以假定引入lambda之后的变量服从正态分布，然后求解极大值的方式推导出lambda，推导过程较为繁琐直接百度即可；

数据平滑技术

移动平均平滑

移动平均平滑是时间序列预测中的一种简单且有效的技术。 它可以用于数据的转换，特征工程，甚至直接用于进行预测；

平滑是一种应用于时间序列的技术，用于消除时间步长之间的细粒度变化。 平滑的目的是消除噪声并更好地暴露潜在因果过程的信号。 移动平均值是在时间序列分析和时间序列预测中使用的一种简单且常见的平滑类型。 计算移动平均值涉及创建一个新序列数据，其中的值变成了原始观测值的某个时间窗口下的平均值。

原始时间序列。 移动平均数要求您指定一个称为窗口宽度的窗口大小。 这定义了用于计算移动平均值的原始观测值的数量。

移动平均平滑主要分为两种：

1、 中心移动平均线

将时间（t）的值计算为时间（t）之前和之后的原始观测值的平均值。 例如，窗口为3的中心移动平均值将计算为：

中心移动平均线ma（t）=平均值（obs（ t 1），obs（t），obs（t + 1））

此方法需要了解将来的值，因此可用于时间序列分析以更好地理解数据集。 中心移动平均线可以用作从时间序列中删除趋势和季节成分的一般方法，但是需要注意，因为计算的时候涉及到未来的数据，因此我们在预测时经常无法使用的方法。（无法使用未来数据来预测）

举个例子，假设我们的序列数据为[1,2,3.....100]，我们以 50 为例，假设窗口为3，则经过中心移动平均平滑之后，50这个点替换为了(47+48+49+50+51+52+53)/7，其它的点依次类推；

2、追踪移动平均线

将时间（t）的值计算为时间（t）以及之前的原始观测值的平均值。 例如，窗口为3的尾随移动平均线将计算为：

trace ma（t）=平均值（obs（ t2），obs（t 1），obs（t））

追踪移动平均线仅使用历史观测值，可以用于时间序列预测，也可以作为特征工程的一种手段，作为特征工程的时候其实就是我们前面说到的时间窗特征工程的方法；

from pandas import read_csv
from matplotlib import pyplot
series = read_csv('daily-total-female-births-CA.csv')
# tail-rolling average transform
series=series.births
rolling = series.rolling(window=3)
rolling_mean = rolling.mean()
print(rolling_mean.head(10))
# plot original and transformed dataset
series.plot()
rolling_mean.plot(color='red')
pyplot.show()
# zoomed plot original and transformed dataset
series[:100].plot()
rolling_mean[:100].plot(color='red')
pyplot.show()

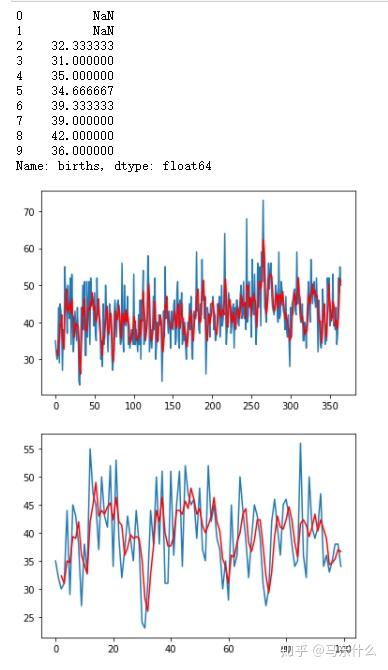
使用移动平均的方式引入新特征的方法我们前面其实已经介绍过了，移动平均可以搭配lag算子一起使用：

import pandas as pd
df = DataFrame(series.values)
width = 3
lag1 = df.shift(1)
lag3 = df.shift(width - 1)
window = lag3.rolling(window=width)
means = window.mean()
dataframe = pd.concat([means, lag1, df], axis=1)
dataframe.columns = ['mean', 't', 't+1']
print(dataframe.head(10))

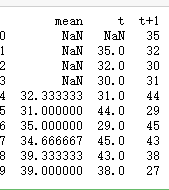
下面介绍一下使用移动平均进行预测：

移动平均线作为预测

移动平均值也可以直接用于预测。 这是一个简单的模型，需要注意的是，和arima这类经济学经典统计模型一样，移动平均模型可以轻松地以滚动预测的方式进行预测， 随着提供新的观测值（例如每天），可以更新模型并为第二天做出预测。 我们可以在Python中手动实现此功能。以下是以移动方式使用的移动平均模型的示例。

from math import sqrt
from pandas import read_csv
from numpy import mean
from sklearn.metrics import mean_squared_error
from matplotlib import pyplot
series = read_csv('daily-total-female-births-CA.csv')
# prepare situation
X = series.births.values
window = 3
history = [X[i] for i in range(window)]
test = [X[i] for i in range(window, len(X))]
predictions = list()
# walk forward over time steps in test
for t in range(len(test)):
    length = len(history)
    yhat = mean([history[i] for i in range(length-window,length)])
    obs = test[t]
    predictions.append(yhat)
    history.append(obs)
print('predicted=%f, expected=%f' % (yhat, obs))
rmse = sqrt(mean_squared_error(test, predictions))
print('Test RMSE: %.3f' % rmse)
# plot
pyplot.plot(test)
pyplot.plot(predictions, color='red')
pyplot.show()
# zoom plot
pyplot.plot(test[:100])
pyplot.plot(predictions[:100], color='red')
pyplot.show()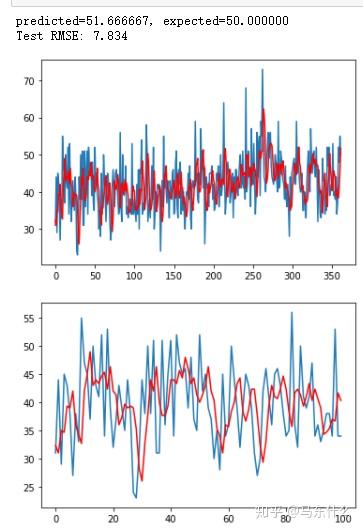

其实思路也很简单，假设我们的训练集数据是

[1,2,3,4,5,6]，然后我们要预测未来的5天的数据，则使用移动平均的方法，假设窗口设置为3，那么 4 5 6的均值为5，则我们预测第7个数字为5，此时，移动窗口，变成了5 6 5，均值为16/3=5.333,然后继续滑动，变成了[6 5 5.33]，依次类推。。。。非常简单粗暴，这种方法和seq2seq一样，存在误差累积的问题，因此不太建议用于中长周期的forecasting，精度可能会比较差，做单步预测靠谱点

白噪声：

如果变量是独立的且均值为零，并且分布相同，则时间序列为白噪声。 这意味着所有变量都具有相同的方差，并且每个值与序列中的所有其他值不存在相关性， 如果序列中的变量是从高斯分布中提取的，则该序列称为高斯白噪声。

为什么白噪声如此重要？

白噪声是时间序列分析和预测中的重要概念。这很重要，主要有两个原因：

1、可预测性：如果时间序列是白噪声，那么根据定义，它是随机的。我们无法合理地对其建模并做出预测。

2、模型诊断：时间序列预测模型中的一系列误差最好是白噪声。

模型诊断是时间序列预测的重要分析手段，一般来说，假设我们的预测结果为信号(t)，则我们可以将原始数据表示成这样：

y（t）=信号（t）+噪声（t）

通过时间序列预测模型进行预测后，就可以对噪声（其实就是残差）进行收集和分析。理想的预测误差序列应该是白噪声。当预测误差是白噪声时，这意味着模型已利用了时间序列中的所有信号信息，以便进行预测。剩下的就是无法建模的随机波动。模型预测不是白噪声的迹象表明对预测模型的进一步改进是可能的。

那么如何确定序列数据是否是白噪声序列？

1、自相关图

from random import gauss
from random import seed
from pandas import Series
from pandas.plotting import autocorrelation_plot
from matplotlib import pyplot
# seed random number generator
seed(1)
# create white noise series
series = [gauss(0.0, 1.0) for i in range(1000)]
series = Series(series)
#Finally, we can create a correlogram and check for any autocorrelation with lag variables.
# autocorrelation
autocorrelation_plot(series)
pyplot.show()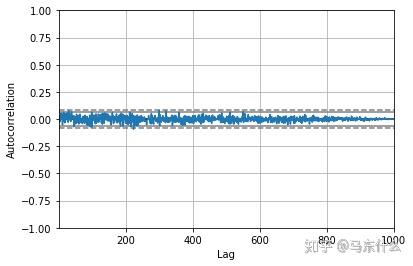

相关图没有显示任何明显的自相关模式。 在95％和99％的置信度之上有一些峰值，但这是统计上的偶然。

from random import gauss
from random import seed
from pandas import Series
from pandas.plotting import autocorrelation_plot
from matplotlib import pyplot
# seed random number generator
seed(1)
# create white noise series
series = [gauss(0.0, 1.0) for i in range(1000)]
series = Series(series)
# summary stats
print(series.describe())
# line plot
series.plot()
pyplot.show()
# histogram plot
series.hist()
pyplot.show()
# autocorrelation
autocorrelation_plot(series)
pyplot.show()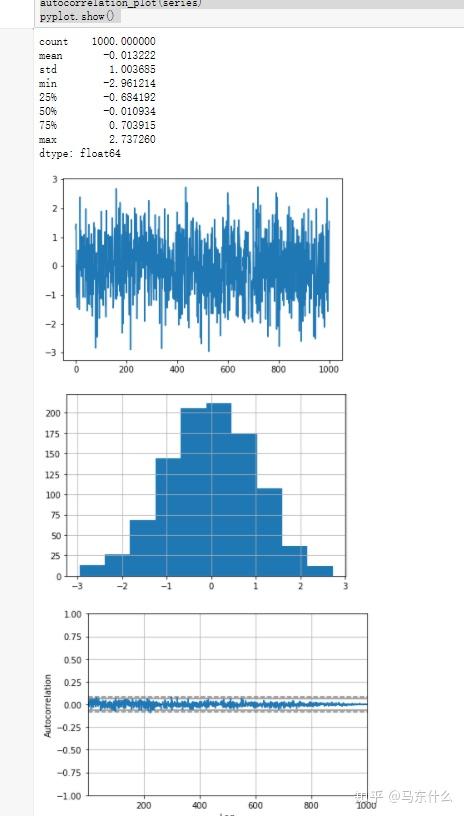

不过这种通过肉眼观察的方法并不是很方便，实际上我们可以通过adf检验来检验序列是否是白噪声；

from pandas import read_csv
from statsmodels.tsa.stattools import adfuller
X = series.passengers.values.astype(float)
result = adfuller(X)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value in result[4].items():
    print(key,value)

这里涉及到两个概念：

一个是时间序列的平稳性问题，一个是adfuller的原理问题：

时间序列数据的平稳性

时间序列不同于更传统的分类和回归预测建模问题。时间结构的数据是存在序列依赖性的。这意味着，有关这些观察结果一致性的重要假设需要特别处理。例如，在进行建模时，存在以下假设：

样本是一致的。在时间序列术语中，我们将此称为时间序列是平稳的。这些假设在时间序列上很容易被违背，例如趋势，季节性和其他随时间变化的结构的影响，例如：

# load time series data
from pandas import read_csv
from matplotlib import pyplot
series = read_csv('daily-total-female-births-CA.csv')
series.plot()
pyplot.show()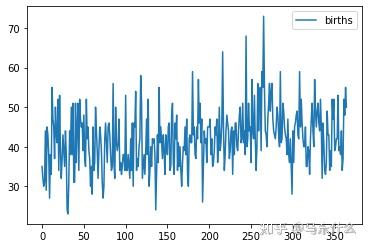

来自非平稳时间序列的观察结果显示了季节性影响，趋势和其他依赖于时间指数的结构。 汇总统计数据（例如均值和方差）确实会随着时间发生变化。 经典的时间序列分析和预测方法涉及通过识别和消除趋势以及消除季节性影响来使非平稳时间序列数据转化为平稳序列。 下面是一个非平稳的航空旅客数据集示例，其中显示了趋势和季节组成部分。

from pandas import read_csv
from matplotlib import pyplot
series = read_csv('airline-passengers.csv')
series.plot()
pyplot.show()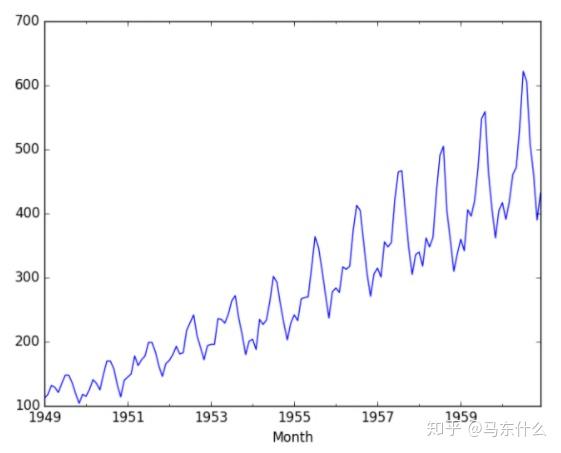

平稳性的一些细节：

1、平稳过程：生成一系列平稳观测值的过程。

2、平稳模型：描述一系列平稳观测值的模型。

3、趋势平稳：不具有趋势的时间序列。

4、季节性（周期性）平稳：不显示周期性的时间序列

5、严平稳：固定过程的数学定义，特别是观测值的联合分布不随时间变化。

这里补充一下严平稳和弱平稳的定义：

一般而言，时间序列被看作一个随机过程{Xt}：
严平稳：多元联合分布保持不变，例如我们假设(X1,X2,X3)是个三维随机变量，（X3,X4,X5)也是个三维随机变量，严平稳要求任何形如（Xn-1,Xn,Xn+1)的三维随机变量分布都是一样的。当然不仅仅是三维，而是任何维的随机变量分布不变。严平稳表示的分布不随时间的改变而改变。研究第1到第n个随机变量跟第2到第n+1个随机变量性质是一样的。
最简单的例子，白噪声（正态），无论怎么取，都是期望为0，方差为1，协方差都为0的n维正态分布，显然，严平稳是非常理想的概念，其实即使是白噪声，如果我们的样本点不多，或者是所取得多元联合分布的n很小，也大概率不会得到期望为0，方差为1，协方差都为0的分布数据；

因此一般我们在时间序列预测问题中主要以弱平稳假设为主：

弱平稳要求序列数据不能有趋势、不能有周期性：

一阶矩就是期望值，二阶(非中心)矩就是对变量的平方求期望，二阶中心矩就是对随机变量与均值(期望)的差的平方求期望。为什么要用平方，因为如果序列中有负数就会产生较大波动，而平方运算就好像对序列添加了绝对值，这样更能体现偏离均值的范围。

通常，如果在时间序列中具有明确的趋势和季节性，需要将其从观测值中删除，然后对残差进行训练。

如果我们将固定模型拟合到数据，则假定我们的数据是固定过程的实现。因此，我们进行分析的第一步应该是检查是否存在任何趋势或季节性影响的证据，如果有，请删除它们。
—第122页，《基于R语言的时间序列预测》。

统计时间序列方法甚至现代机器学习方法都将受益于数据中更清晰的信号。但当经典的经济学方法失败时，我们转向机器学习方法。当我们想要更多或更好的结果。我们不知道如何对时间序列数据中的未知非线性关系进行最佳建模，并且某些问题可能是平稳序列数据和非平稳序列数据的混合。

这里，当我们使用机器学习方法的时候，建议是将时间序列的平稳或者不平稳的属性视为另一种信息源，通过特征工程的方式将这种信息表征出来；

前面提到了自相关图，肉眼观察平稳性，下面介绍更加科学的方法，adfuller检验：

from pandas import read_csv
from statsmodels.tsa.stattools import adfuller
X = series.passengers.values.astype(float)
result = adfuller(X)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value in result[4].items():
    print(key,value)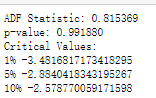

adfuller函数的参数意义分别是：

1. x：一维的数据序列。
2. maxlag：最大滞后数目。
3. regression：回归中的包含项（c：只有常数项，默认；ct：常数项和趋势项；ctt：常数项，线性二次项；nc：没有常数项和趋势项）
4. autolag：自动选择滞后数目（AIC：赤池信息准则，默认；BIC：贝叶斯信息准则；t-stat：基于maxlag，从maxlag开始并删除一个滞后直到最后一个滞后长度基于 t-statistic 显著性小于5%为止；None：使用maxlag指定的滞后）
5. store：True False，默认。
6. regresults：True 完整的回归结果将返回。False，默认。

回值意义为：

1. adf：Test statistic，T检验，假设检验值。
2. pvalue：假设检验结果。
3. usedlag：使用的滞后阶数。
4. nobs：用于ADF回归和计算临界值用到的观测值数目。
5. icbest：如果autolag不是None的话，返回最大的信息准则值。
6. resstore：将结果合并为一个dummy

关于adf检验的介绍可见：实际上就是针对原始序列数据和滞后数据的方程的单位根求解

时间序列应用的验证和评估

时间序列数据的模型评估与评估指标之前都写过，这里直接贴链接：

误差分析：

可视化残余预测误差

时间序列回归问题的预测误差称为残差或残差。探索时间序列预测问题上的残差可以告诉您很多有关您的预测模型，甚至提出改进建议。

时间序列预测问题的预测误差称为残差。计算为预期结果减去预测值，通常，在分析残差时，我们在寻找模式或结构。模式的迹象表明错误不是随机的而我们期望残留误差是随机的，因为这意味着模型已捕获所有的时序结构，剩下的唯一误差是时间序列中的随机波动，这是无法建模的。模式或结构的迹象表明有更多信息模型可以捕获并用于做出更好的预测。实际上这也是常规的机器学习问题中重要的 误差分析。

下面我们用一个简单的例子来看看如何分析：

# create lagged dataset
values = DataFrame(series.values)
dataframe = concat([values.shift(1), values], axis=1)
dataframe.columns = ['t;, 't+1']
# split into train and test sets
X = dataframe.values
train_size = int(len(X) * 0.66)
train, test = X[1:train_size], X[train_size:]
train_X, train_y = train[:,0], train[:,1]
test_X, test_y = test[:,0], test[:,1]
# persistence model
predictions = [x for x in test_X]
# line plot of residual errors
from pandas import read_csv
from pandas import DataFrame
from pandas import concat
from matplotlib import pyplot
series = read_csv(✬daily-total-female-births.csv✬, header=0, index_col=0, parse_dates=True,
squeeze=True)
# create lagged dataset
values = DataFrame(series.values)
dataframe = concat([values.shift(1), values], axis=1)
dataframe.columns = ['t', 't+1']
# split into train and test sets
X = dataframe.values
train_size = int(len(X) * 0.66)
train, test = X[1:train_size], X[train_size:]
train_X, train_y = train[:,0], train[:,1]
test_X, test_y = test[:,0], test[:,1]
# persistence model
predictions = [x for x in test_X]
# calculate residuals
residuals = [test_y[i]-predictions[i] for i in range(len(predictions))]
residuals = DataFrame(residuals)
# plot residuals
residuals.plot()
pyplot.show()

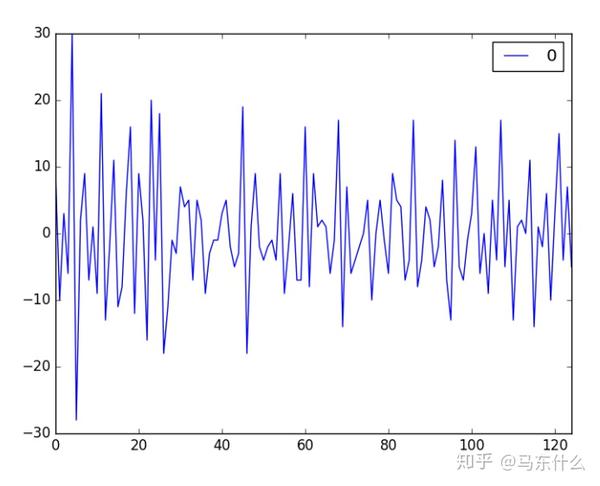
我们可以计算残留误差的摘要统计信息。 首先，我们对残差的平均值感兴趣。 接近零的值表示预测中没有偏差，

而正值和负值表明所做的预测中存在正向或负向偏差。 了解预测中的偏差很有用，因为可以事先在预测中进行更正对其使用或评估。 以下是计算残留误差分布的摘要统计信息的示例。这包括分布的平均值和标准偏差，百分位数以及观察到的最小和最大误差。

残差直方图和密度图

除了汇总统计信息外，还可以使用图表更好地理解错误的分布。我们希望预测误差在零均值附近呈正态分布。

from pandas import read_csv
from pandas import DataFrame
from pandas import concat
from matplotlib import pyplot
series = read_csv(✬daily-total-female-births.csv✬, header=0, index_col=0, parse_dates=True,
squeeze=True)
# create lagged dataset
values = DataFrame(series.values)
dataframe = concat([values.shift(1), values], axis=1)
dataframe.columns = [✬t✬, ✬t+1✬] # split into train and test sets
X = dataframe.values
train_size = int(len(X) * 0.66)
train, test = X[1:train_size], X[train_size:]
train_X, train_y = train[:,0], train[:,1]
test_X, test_y = test[:,0], test[:,1]
# persistence model
predictions = [x for x in test_X]
# calculate residuals
residuals = [test_y[i]-predictions[i] for i in range(len(predictions))]
residuals = DataFrame(residuals)
# histogram plot
residuals.hist()
pyplot.show()
# density plot
residuals.plot(kind=✬kde✬)
pyplot.show()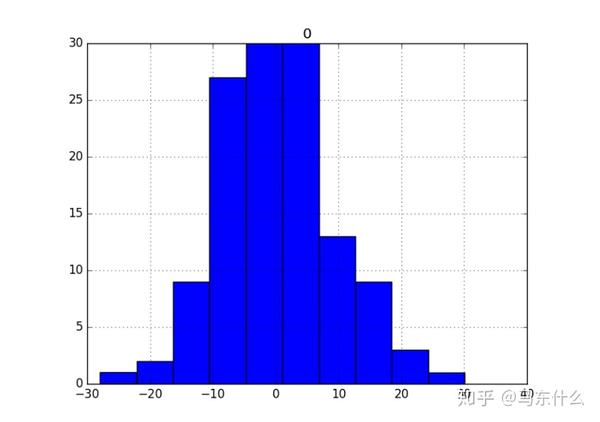

我们可以看到分布确实具有高斯外观，但可能更尖锐，显示出一些不对称的指数分布。 如果hist显示分布显然是非高斯的，这表明建模的假设流程可能不正确，可能需要使用其他建模方法。 一个大的偏斜可能暗示在建模之前需要对序列数据执行转换，例如取log或平方根。

残差的Q-Q图

Q-Q图或分位数图比较两个分布，可用于查看相似度， 我们可以使用qqplot（）函数创建一个Q-Q图，Q-Q图可用于快速检查残差分布的正态性。这些值被排序，并与理想的高斯分布进行比较。

# qq plot of residual errors
from pandas import read_csv
from pandas import DataFrame
from pandas import concat
from matplotlib import pyplot
import numpy
from statsmodels.graphics.gofplots import qqplot
series = read_csv(✬daily-total-female-births.csv✬, header=0, index_col=0, parse_dates=True,
squeeze=True)
# create lagged dataset
values = DataFrame(series.values)
dataframe = concat([values.shift(1), values], axis=1)
dataframe.columns = [✬t✬, ✬t+1✬] # split into train and test sets
X = dataframe.values
train_size = int(len(X) * 0.66)
train, test = X[1:train_size], X[train_size:]
train_X, train_y = train[:,0], train[:,1]
test_X, test_y = test[:,0], test[:,1]
# persistence model
predictions = [x for x in test_X]
# calculate residuals
residuals = [test_y[i]-predictions[i] for i in range(len(predictions))]
residuals = numpy.array(residuals)
qqplot(residuals, line=✬r✬)
pyplot.show()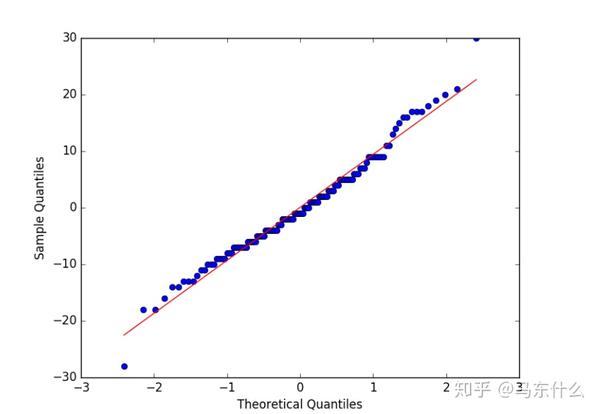

残差自相关图

自相关计算先前时间步长处观测值与观测值之间关系的强度。我们可以计算残留误差时间序列的自相关并绘制结果。这称为自相关图。我们不希望有残差之间的任何相关性。这将通过自相关分数表示低于显着性阈值 残差图中的显着自相关表明该模型可能正在更好地结合观察与滞后观察之间的关系，这称为自回归。

from pandas import concat
from matplotlib import pyplot
from pandas.plotting import autocorrelation_plot
series = read_csv(✬daily-total-female-births.csv✬, header=0, index_col=0, parse_dates=True,
squeeze=True)
# create lagged dataset
values = DataFrame(series.values)
dataframe = concat([values.shift(1), values], axis=1)
dataframe.columns = [✬t✬, ✬t+1✬] # split into train and test sets
X = dataframe.values
train_size = int(len(X) * 0.66)
train, test = X[1:train_size], X[train_size:]
train_X, train_y = train[:,0], train[:,1]
test_X, test_y = test[:,0], test[:,1]
# persistence model