【有限元学习笔记13】deal.II有限元库step-6例程学习
The step-6 tutorial program of deal.II: Adaptive meshes.
本文章展示了如何使用自适应网格细化和上一篇文章讨论的约束条件来解决拉普拉斯方程。我们展示了处理自适应网格所需的 10 或 15 行额外代码。尽管在这种情况下查看网格的方式完全不同,但程序的其余部分并没有改变。
在代码中,我细化了
30%
的单元,粗化了
3%
。这些"神奇"的数字是有目的的:在2D中,如果你细化炼了
N
个单元中的一小部分
x
,那么你就用它们的四个子单元替换这些单元,所以你在下一轮将得到总共
(1-x)N+4xN=(1+3x)N \\
个单元。因此,
x=30%
可以确保我们下次得到大约
两倍
的单元。用于粗化的
3%
的部分足够小,这样就不会有很多之前被细化的单元被再次粗化,但对于抵消我们所犯的错误来说也足够大了。
当然,这就引出了一个问题:为什么在每次细化时将单元格的数量增加一倍是有用的。为了理解这个问题,让我们假设我们在最终的网格上有 M 个单元。那么我们在之前的迭代中,网格上有 M/2, M/4, M/8, ... 个单元。如果我们有一个完美的求解器,求解一个有 M 个未知数的线性系统需要花费 O(M) 次运算,那么在一个总是加倍的网格序列上求解将花费的总计算时间为
...+O(M/8)+O(M/4)+O(M/2)+O(M)=O(2M) \\
次运算,或者大约是最好的网格所需时间的两倍——鉴于我们可能已经通过适应性细化构建了一个好网格,这个惩罚不算太大。
另一方面,如果我们选择了一个远小于
30%
的分数
x
(也就是说,我们在细化网格时非常小心),那么我们可能会有一个稍微好一点的网格(也就是说,自由度
M
更小),但
所需的总计算时间会更大
(达到同样精度)。另一方面,如果我们选择
x=1
(即全局细化),那么我们可能会有一个完全不适合解的网格(即:我们需要一个非常大的
M
来获得一个还可以的精度),计算时间的总和将是
...+O(M/32)+O(M/8)+O(M/4)+O(M)=O(4M/3) \\
即使在最好的情况下(意味着全局细化网格就是所需要的最好情况)也只比 x=30% 的自适应细化快三分之一。
值得注意的是,导致单元数量翻倍的因子 x 在三维中是不同的。
1 step-6主要展示了什么
- 如何 自适应 地 细化 网格
- 如何处理由此产生的 约束
2 介绍
这个程序介绍了
deal.II
的最后一个
主要特点
:
使用自适应(局部)细化网格
。这个程序主要基于
step-4
和
step-5
,而且,正如你将看到的,实际上不需要花太多的代码来实现自适应性。事实上,虽然我们做了大量的解释,但
自适应网格添加到一个现有的程序中
,
只需要十几行额外的代码
(主要是deal.II
封装的好
!)。该程序展示了这些代码应该怎么写,以及自适应网格细化(
AMR
)的另一个重要组成部分:
- 一个可以用来 确定是否有必要细化 一个单元的 标准 :
- 如果单元上面的误差很大,就进行细化;
- 如果单元上面的误差很小,就进行粗化;
- 或者让这个单元保持不变。
2.1 自适应细化的网格是什么样子的
有许多方法可以自适应地细化网格。整个算法的基本结构总是相同的,由以下步骤的循环组成:
- 在当前网格上求解PDE;
- 用某种标准来估计每个单元的误差,这个标准是指示性的;
- 标记那些有大误差的单元进行细化,标记那些有特别小误差的单元进行粗化,其余的不做处理;
- 细化和粗化被标记的单元,以获得一个新的网格;
- 在新的网格上重复上述步骤,直到整体误差足够小。
由于一些可能被历史遗忘的原因(也许是这些函数过去是用FORTRAN语言实现的,这种语言并 不关心某个东西是用小写字母还是大写字母拼写 的,程序员经常 习惯性地选择大写字母 ),上述循环在关于网格适应性的出版物中经常被称为SOLVE-ESTIMATE-MARK-REFINE循环(用这种拼法)。
有多种方法可以实现这一点,它们的区别主要在于如何从前一个网格中生成一个新网格。
如果要使用三角形网格(deal.II没有这样做,因为deal.II中没有三角形网格),那么就有两种基本的可能性:
- 最长边细化 :这很难用语言描述,而且因为deal.II不使用三角形网格,不值得在这里花时间。但如果你很好奇,你可以查看《有限元学习笔记11》。
- 红-绿细化 :这种策略甚至更难用语言描述(你可以查看《有限元学习笔记11》),其优点是 细化不会传播到我们想要细化的单元的领域之外 。然而,它的实施难度要大得多。
这两种方法对2D的四边形和3D的六面体都不起作用。原因是要细化的四边形单元的四边形相邻单元所产生的过渡元素将是 三角形 ,这就导致了单元表面上的节点属于一方,但在另一方是不平衡的。这些节点的常用术语是"悬挂节点",这些网格在一个非常简单的情况下看起来是这样的。
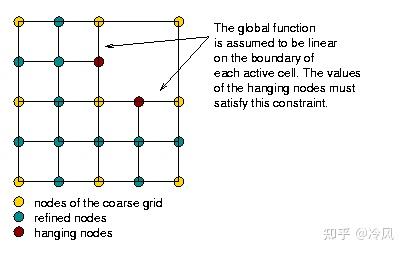
一个更复杂的二维网格看起来是这样的(并在下面的"结果"部分讨论):
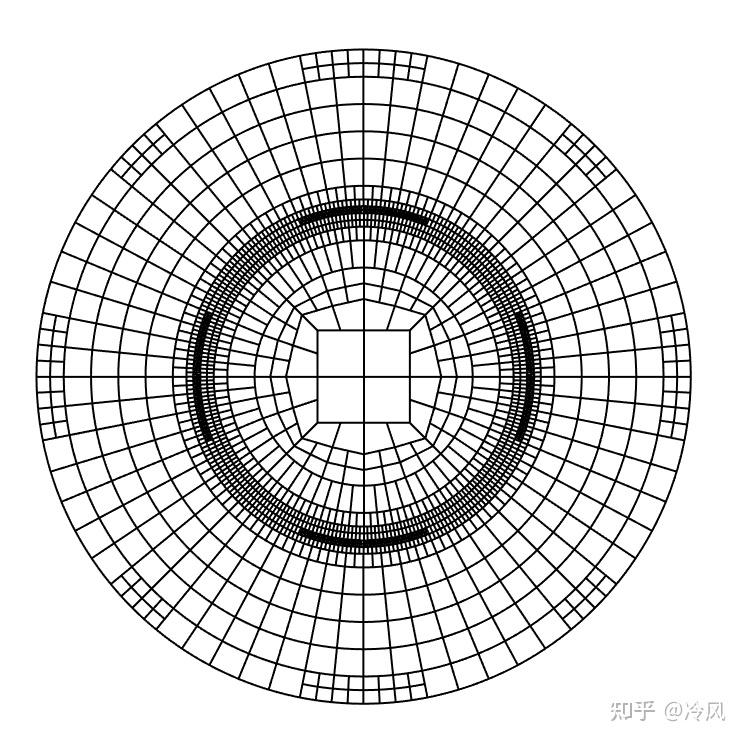
最后,展示一个具有“悬挂节点”的三维网格(来自
step-43
):
2.2 为什么需要自

适应细化网格?
现在你已经看到了这些自适应细化网格的样子,你应该问我们为什么要这样做。毕竟,我们从理论上知道,如果我们对网格进行全局细化,误差会逐渐趋于零,因为:
\Vert (u-u_h)\Vert_\Omega \leq C h_{\max}^p \Vert \nabla^{p+1} u \Vert_\Omega \\
其中 C 是一个与 h 和 u 都无关的常数, p 是有限元中所使用的插值多项式次数, h_{\max} 是最大单元的直径。
那么, 如果最大的单元才是决定因素 ,那么为什么我们还要在域的某些部分将网格做得很细,而不是全部,这岂不是没意义(因为最大单元的尺寸还是很大)?
答案在于上面的误差估计公式不是最佳的。事实上,一些更多的工作表明,以下是一个更好的估计(你应该与上述估计的平方进行比较):
\Vert (u-u_h)\Vert_\Omega^2 \leq C \sum_{K} h_{K}^{2p} \Vert \nabla^{p+1}u \Vert_K \\
这个公式表明, 没有必要让最大的单元格变小 ,而只需要在 \Vert \nabla^{p+1}u \Vert_K 大的地方让单元变小就可以了! 换句话说:只有在 解有较大变化的地方 ,如 p+1 次导数较大的地方,网格才需要进行细化。这具有直观的意义:例如,如果我们使用一个线性元素 p=1 ,那么 即使网格很粗 ,那些 解接近线性 的地方(即 \nabla^2 u 很小), 误差也会很小 。只有那些二阶导数大的地方才会使大的单元求解得很差,因此这就是我们应该把网格做小的地方。
当然,这个 先验估计 在实践中不是很有用,因为我们 不知道问题的精确解 u ,因此,我们无法计算 \nabla^{p+1}u 。所以,我们通常采取的方法是:根据我们之前计算的离散解 u_h 来 计算 $\nabla^{p+1}u的 数值近似值 。
我们将在下面稍微详细地讨论这个问题。这种方法可以帮助我们确定哪些单元具有较大的 p+1 阶导数,然后这些单元就是细化网格的候选单元。
2.3 如何在理论上处理悬挂节点
具体可看《有限元学习笔记12》。
上面提到的用于三角形网格的方法,要花大力气确保每个顶点都是所有相邻单元的顶点——也就是说, 没有悬挂节点 。这就自动确保了我们能够以这样的方式定义形状函数,即它们是 全局连续 的。
如果我们在有悬挂节点的网格上定义形状函数,我们最终可能得到不连续的形状函数。比如,我们考虑一下右上角的单元没有被细化,并使用双线性有限元的情况:

在这种情况下,与悬挂节点相关的形状函数是定义在与每个悬挂节点相邻的两个小单元上。但我们如何将它们扩展到相邻的大单元呢?显然:
- 从大单元一侧看(即右上角的单元),函数对大单元的扩展不能是双线性的,因为那样的话,它需要沿着大单元的每条边都线性化,这意味着它在整条边上需要为零,因为它在大单元的两个顶点上需要为零。
- 但从小单元一侧看,它在悬挂节点上的值并不是零——所以它 不是连续的 。下面三张图显示了沿着有关边缘的三个形状函数,当以通常的方式简单地根据它们相邻的单元格来定义时,这些形状函数变成了不连续的:
- 与悬挂节点相邻的不连续的形状函数
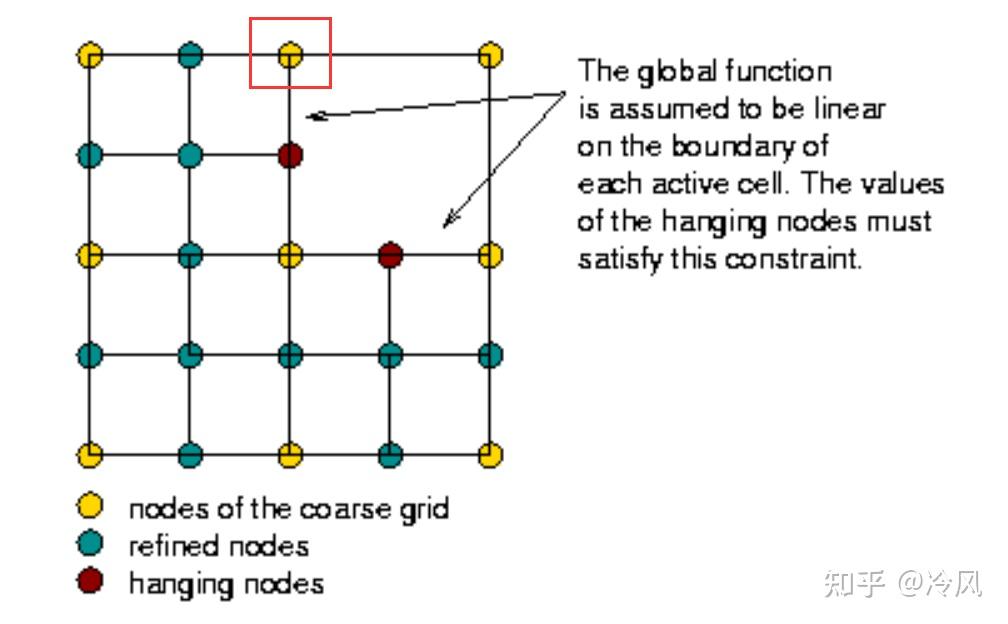

- 悬挂节点处的不连续形状函数
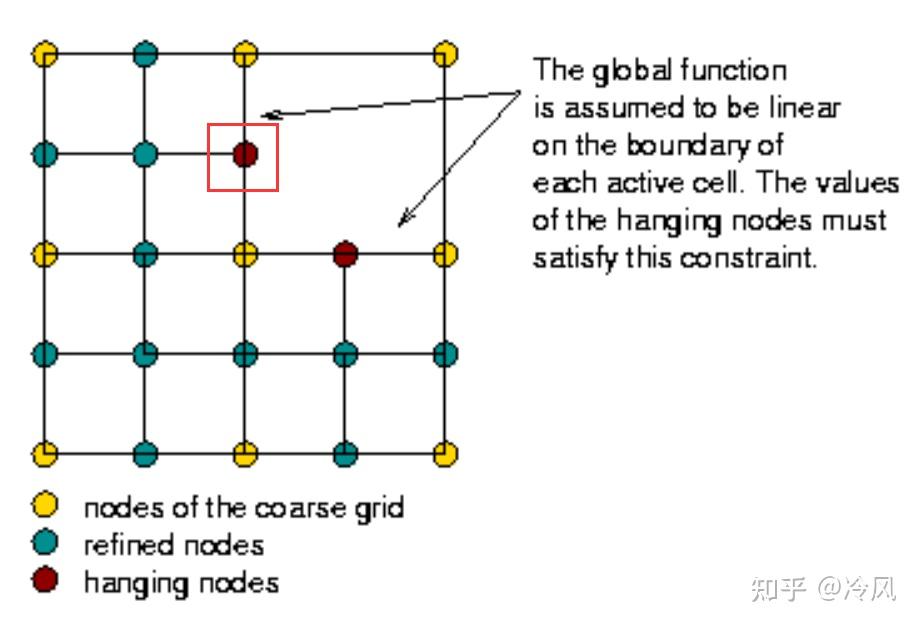
- 与悬挂节点相邻的不连续的形状函数
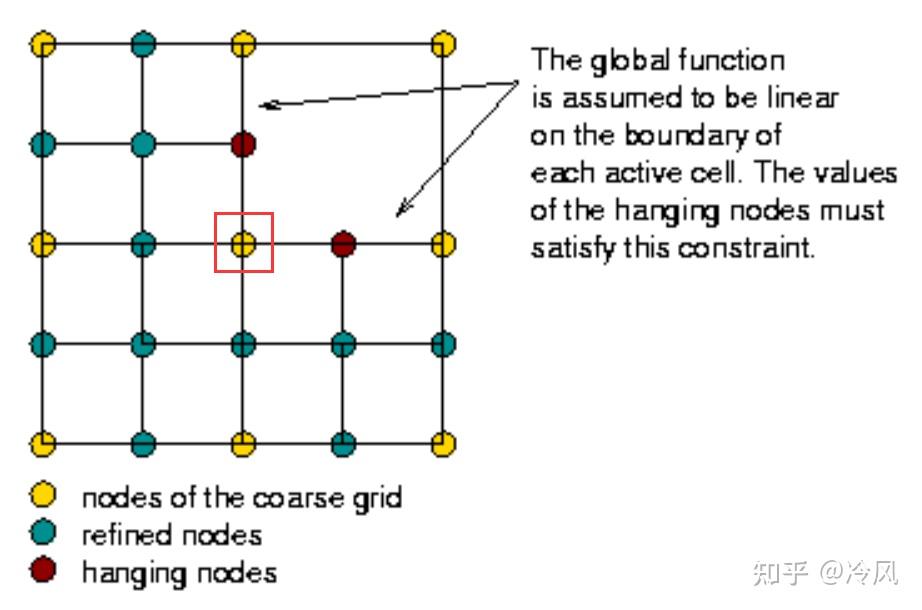

我们知道有限元的解是形函数的线性组合,我们所求的线性方程组的解就是线性组合要用的系数(每个系数对应于一个形函数)。如果随意进行组合的话,有限元的解很可能会是 不连续 的。但我们确实希望 有限元解 是 连续 的,这样我们就有一个"符合要求的有限元方法",其中 离散的有限元空间 是我们所求拉普拉斯方程在 H^1 函数空间解的子集 。为了保证全局解在这些节点上也是连续的,我们必须对这些节点上的解的值提出一些 额外的约束 。
- 诀窍是要认识到,虽然上面显示的 形状函数是不连续的 (因此它们的任意线性组合也是不连续的),但如果系数 U_j 满足某些关系, 形状函数线性组合 起来的 近似解可以是连续 的:
- u_h(x)=\sum_jU_j \phi_j(x) \\
- 换句话说,系数 U_j 不能任意选择,而必须 满足某些约束条件 ,这样,函数 u_h 实际上是连续的。这些约束条件在 概念上比较容易理解 ,但在 软件 中的 实现却很复杂 ,需要几千行的代码。
- 另一方面,在用户代码中,在处理悬挂节点时,你只需要增加大约六行代码。
在下面的程序中,我们将展示如何从
deal.II
中获得这些约束,以及如何在线性方程组的求解中使用它们。
2.4 如何在实践中处理悬挂节点
悬挂节点约束的实践比我们上面概述的理论更简单。实际上,你只需要在
step-4
这样的程序中增加六行额外的代码,就可以使它在有悬挂节点的自适应网格中工作。有趣的是,这
与你要解决的方程完全无关
。这些
约束的代数性质与方程无关
,
只取决于对有限元的选择
。
因此,处理这些约束的代码完全包含在deal.II库本身,你不需要担心细节问题
。
你需要使其发挥作用的步骤基本上是这样的:
-
你必须创建一个
AffineConstraints对象,(顾名思义)它将 存储有限元空间的所有约束 。在目前的情况下,这些约束是由于我们希望 保持解空间的连续 ,即使在有悬挂节点的情况下。(下面我们还将简要地提到,我们还将把边界值放到这个对象中,但这是一个单独的问题)。 -
你必须使用
DoFTools::make_hanging_node_constraints()函数来填充这个对象,以确保有限元空间的元素的连续性。 -
当你通过使用
AffineConstraints::distribution_local_to_global()将局部对矩阵和右手边的贡献复制到全局对象时,你必须使用这个对象。这个函数将约束应用到线性系统中,确保位于悬挂节点的自由度事实上不是真正的自由度(因为是 被约束的自由度 , 不是真正的自由 !)。相反,通过将它们的行和列设置为零,并在对角线上放置一些东西以确保矩阵保持可反转,它们实际上 被从线性系统中消除 了。对于我们在这里解决的拉普拉斯方程来说,这个过程产生的矩阵仍然是 对称和正定 的,所以我们可以继续使用 共轭梯度法 来解决。 -
然后你像往常一样求解线性系统,但在这一步结束时,你需要确保
位于悬挂节点上的"自由度"得到它们正确的(约束)值
,这样你随后可视化的或以其他方式评估的解决方案实际上是连续的。这可以通过在求解后立即调用
AffineConstraints::distribution()来实现。
这四个步骤实际上是所有我们实现自适应网格所需要的——从用户的角度来看就是这么简单。在用户代码中,实际上只有四个额外的步骤。
2.5 如何获得局部细化的网格
既然我们知道如何处理有这些悬挂节点的网格,下一个问题就是如何获得这些节点。
- 如果你知道哪里需要细化网格,那么可以手动进行细化。但是在现实中,我们并不知道哪里需要细化。
- 同时,我们也不知道PDE的精确解(因为,如果我们知道,我们就不必使用有限元方法),因此我们更不可能知道哪里需要增加局部网格细化来更好地解决解有强烈变化的地方( p+1 阶导数值大的地方)。
- 但是上面的讨论表明,也许我们可以用一个网格上的 离散解 来 估计 导数 \nabla^{p+1}u ,然后用这个来确定哪些单元太大,哪些已经足够小。
- 然后我们可以 用局部网格细化方法 从当前的网格中 生成一个新的网格 。如果有必要,这个步骤会重复进行,直到我们对我们的数值解感到满意——或者,更常见的是,直到我们耗尽了计算资源(内存不足)或耐心。
所以这
正是我们要做
的。局部细化网格是使用
误差估计器
产生的,该估计器估计了拉普拉斯算子的数值解的
能量误差
。由于它是由
Kelly
和他的同事开发的,我们经常把这个误差估计器称为"
Kelly
细化指标"。实现它的类被称为
KellyErrorEstimator
,在该类的文档中可以找到大量的信息,这里不需要重复。
总结一下,这个类计算一个向量,该向量的大小与活动单元(active cells)的数量一样多,而且每个分量都对应于一个单元的误差估计值。然后使用这个估计值来细化网格的单元格: 那些有较大误差的单元将被标记为细化,那些有特别小的估计值的单元将被标记为粗化。我们不需要用手去做这些:一旦我们获得了误差估计矢量,命名空间
GridRefinement
中的函数将为我们完成这一切。
2.6 边界条件
事实证明,人们可以把Dirichlet边界条件看作是对自由度的另一种约束。这的确是一个特别简单的约束。如果 j 是边界上的一个自由度,其位置为 \mathbf{x}_j ,那么在 \partial \Omega 上施加边界条件 u=g ,就可以得到约束 U_j=g(\mathbf{x}_j) 。
AffineConstraints
类也可以处理这样的约束,这使得我们可以用处理悬挂节点约束的对象同时也处理这些Dirichlet边界条件。这样一来,我们就不需要在装配后再应用边界条件(就像我们在前面的步骤中做的那样)。所有需要的是,我们调用
VectorTools::interpolate_boundary_values()
的变体,在
AffineConstraints
对象中返回其信息,而不是我们在以前的教程程序中使用的
std::map
。
2.7 这个程序展示的其他新内容
由于用于局部细化网格的概念非常重要,我们在这个例子中没有展示很多其他材料。
一个例外是,我们展示了如何
使用双二次单元
而不是之前所有例子中使用的
双线性单元
。事实上,
使用高阶元素只需替换程序中的三行
,即在这个程序的主类的构造函数中初始化
fe
成员变量,以及在两个地方使用适当的正交公式。程序的其他部分没有变化。
其他唯一的新东西是一个在主函数中捕捉异常的方法,以便在程序因某种原因崩溃时输出一些信息(方便进行Debug)。下面将详细讨论这个问题。
3 程序解读
3.1 头文件
前面几个文件已经在前面的例子中讲过了,因此不再进一步评论。
#include <deal.II/base/quadrature_lib.h>
#include <deal.II/dofs/dof_handler.h>
#include <deal.II/dofs/dof_tools.h>
#include <deal.II/fe/fe_values.h>
#include <deal.II/grid/tria.h>
#include <deal.II/grid/grid_generator.h>
#include <deal.II/lac/dynamic_sparsity_pattern.h>
#include <deal.II/lac/full_matrix.h>
#include <deal.II/lac/precondition.h>
#include <deal.II/lac/solver_cg.h>
#include <deal.II/lac/sparse_matrix.h>
#include <deal.II/lac/vector.h>
#include <deal.II/numerics/data_out.h>
#include <deal.II/numerics/vector_tools.h>
#include <fstream>
从下面的include文件中我们将导入
H1-conforming
有限元形状函数的声明。这个系列的有限元被称为
FE_Q
,在
之前
的所有例子中已经
用于定义通常的双线性或三线性单元
,但我们现在将把它用于
双二次单元
:
#include <deal.II/fe/fe_q.h>
我们不会像前面的例子那样从文件中读取网格,而是使用库的一个函数来生成网格。然而,我们将希望在每次细化后都输出局部细化完成后的网格(只是网格,而不是解),所以我们需要以下include文件,而不是
grid_in.h
:
#include <deal.II/grid/grid_out.h>
当使用局部细化网格时,我们会得到所谓的悬挂节点。然而, 标准的有限元方法假定离散的解空间是连续的 ,所以我们需要确保悬挂节点上的自由度符合一些约束条件,从而使全局解是连续的。我们也要在这个对象中存储边界条件。下面的文件包含一个用来处理这些约束条件的类:
#include <deal.II/lac/affine_constraints.h>
为了对我们的网格进行局部细化,我们需要一个来自库的函数, 根据 我们计算的 误差指标决定哪些单元需要细化或粗化 。这个函数定义在这里:
#include <deal.II/grid/grid_refinement.h>
最后,我们需要一个简单的方法来实际计算基于某种误差估计的细化指标。虽然一般来说,适应性是非常具体的问题,但以下文件中的误差指标往往可以为一类广泛的问题产生相当好的适应性网格。
#include <deal.II/numerics/error_estimator.h>
最后,这和以前的方案一样,使用
deal.II
的命名空间:
using namespace dealii;
3.2
Step6
类模板
主类也是几乎没有变化的。然而,我们增加了两项内容:我们增加了
refine_grid
函数,该函数用于
自适应地细化网格
(而不是前面例子中的全局细化),还有一个变量,它将保存约束。
template <int dim>
class Step6
public:
Step6();
void run();
private:
void setup_system();
void assemble_system();
void solve();
void refine_grid
();
void output_results(const unsigned int cycle) const;
Triangulation<dim> triangulation;
FE_Q<dim> fe;
DoFHandler<dim> dof_handler;
这是主类中的新变量。我们需要一个
AffineConstraints
类的对象
constraints
,它持有一个
约束条件的列表
,从而保存悬挂节点和边界条件。
AffineConstraints<double> constraints; // 存放约束信息
SparseMatrix<double> system_matrix; // 系统矩阵对象
SparsityPattern sparsity_pattern; // 存储非零位置对象
Vector<double> solution; // 解向量
Vector<double> system_rhs; // 右手边向量
3.3 非恒定系数
非恒定系数的实现是逐字复制自
step-5
。
template <int dim>
double coefficient(const Point<dim> &p)
if (p.square() < 0.5 * 0.5) // 对II范数进行判断
return 20; // 在半径0.5的范围内就返回系数值20
return 1; // 在半径0.5的范围外就返回系数值1
3.4
Step6
类的构造函数
Step6::Step6
这个类的构造函数与之前的基本相同,但这一次我们想使用二次单元。要做到这一点,我们只需要用所需的多项式次数(这里是
2
)替换构造函数参数(在之前的所有例子中是
1
)。
template <int dim>
Step6<dim>::Step6() // 使用 : 的作用是表示后面为初始化列表
: fe(2) // 使用二次Lagrange单元
, dof_handler(triangulation) // // 将网格对象绑定至dof_handler
3.5 预处理系统
Step6::setup_system
下一个函数设置了所有描述线性有限元问题的变量,如
DoFHandler
、矩阵和向量。与我们在第5步所做的不同的是,我们现在还必须处理悬挂节点约束。这些约束几乎完全由库来处理,也就是说,你只需要知道它们的存在以及如何获得它们,但你不必知道它们是如何形成的,也不必知道对它们到底做了什么。
在函数的开头,你会发现所有的事情都和
step-5
一样:设置自由度(这次我们有二次单元,但是从用户代码的角度来看,和线性——或者任何其他阶次的情况——没有区别),生成稀疏模式,初始化解和右手边的向量。请注意,现在每行的稀疏模式将有更多的条目,因为现在每个单元有9个自由度,而不是只有4个(这里采用的是Lagrange插值单元,所以二阶单元有9个自由度),它们可以相互耦合。
小插曲 :在单元内部增加节点由于不能构成完全多项式,所以一般无法显著提高精度; 而在边界增加节点则更容易构成完全多项式,有助于提高精度。在边界增加节点的四边形单元叫做Serendipity矩形单元,这个单元的二阶单元就只有8个自由度了,但可以和9自由度的Lagrange单元获得相似的精度!
template <int dim>
void Step6<dim>::setup_system()
dof_handler.distribute_dofs(fe); // 为Triangulation分配自由度
solution.reinit(dof_handler.n_dofs()); // 调整解向量大小
system_rhs.reinit(dof_handler.n_dofs()); // 调整右手边向量大小
我们现在可以用悬挂节点的约束来填充
AffineConstraints
对象。由于我们将在每一个循环中都调用这个函数,所以我们首先要清除上一个系统中的约束集,然后计算新的约束。
constraints.clear(); // 清除上一次循环中所求解系统的约束
DoFTools::make_hanging_node_constraints(dof_handler, constraints); // 计算新的约束
现在我们已经准备好用指标
0
来插值边界值(在整个边界上进行),并将得到的约束存储在我们的
constraints
对象中。请注意,我们并不像在前面的步骤中那样,在装配后应用边界条件:相反,我们把我们的函数空间上的所有约束都放在
AffineConstraints
类型的对象
constraints
中。我们可以以任何顺序向
AffineConstraints
类型的对象
constraints
添加约束:如果
两个约束发生冲突
,那么约束矩阵要么
中止
,要么通过
Assert
宏
抛出一个异常
。
VectorTools::interpolate_boundary_values(dof_handler,
Functions::ZeroFunction<dim>(), // 使用 0 函数进行插值
constraints); // 边界条件值计算
在所有约束条件被添加后,需要对它们进行
排序和重新排列
,以更有效地执行一些动作。这种
后处理
是通过
close()
函数完成的,
之后就不能再添加任何约束
。
constraints.close(); // 后处理,对约束进行排序,提升效率
现在我们首先建立我们的压缩稀疏度模式,就像我们在前面的例子中做的那样。尽管如此,我们并没
有立即将其复制到最终的稀疏度模式
中。请注意,我们调用了
make_sparsity_pattern
的一个变体,它将
AffineConstraints
类型的对象
constraints
作为第三个参数。我们通过将参数
keep_constrained_dofs
设置为
false
(换句话说,我们永远不会写进矩阵中对应于受限自由度的条目),让该例程知道我们永远不会写进由
constraints
给出的位置。如果我们在装配后对约束条件进行压缩,我们就必须传递
true
,因为这样我们就会首先写入这些位置,然后
在压缩过程中
再次
将它们设置为零
。
DynamicSparsityPattern dsp(dof_handler.n_dofs()); // 中间对象,防止内存浪费
DoFTools::make_sparsity_pattern(dof_handler,
dsp,
constraints,
/*keep_constrained_dofs = */ false); // 创建稀疏模式
现在,矩阵的所有非零元素都是已知的(即那些来自常规组装矩阵的元素和那些通过消除约束引入的元素)。我们可以将我们的中间对象复制到稀疏模式中。
sparsity_pattern.copy_from(dsp); // 从dsp中创建实际的稀疏性模式
最后,我们初始化稀疏矩阵:
system_matrix.reinit(sparsity_pattern); // 调整系统稀疏矩阵大小
3.6 组装系统函数
Step6::assemble_system
接下来,我们要组装矩阵。然而,为了将每个单元格上的本地矩阵和向量复制到全局系统中,我们不再使用手写的循环。相反,我们使用
AffineConstraints::distribut_local_to_global()
,它在内部执行这个循环,同时为对应于
受约束自由度的行和列
进行
高斯消除
。
构成局部贡献的其他代码保持不变。然而,值得注意的是,在底层中有几处地方与以前不同。首先,由于采用了二次单元,函数
dofs_per_cell
和
quadrature_formula.size()
的返回值现在都为
9
,而之前是
4
。引入这样的变量作为缩写是一个很好的策略,可以使代码在不同的元素下工作,而不需要改变太多的代码。其次,
fe_values
对象当然也需要做其他事情,因为现在的形状函数在每个坐标变量中都是二次函数,而不是线性的。不过,这也是
完全由库来处理
的事情。
template <int dim>
void Step6<dim>::assemble_system()
const QGauss<dim> quadrature_formula(fe.degree + 1); // 正交公式的阶数比有限元阶数多1
// 需要有update_quadrature_points标志,否则无法计算每个单元上系数的值
FEValues<dim> fe_values(fe,
quadrature_formula,
update_values | update_gradients |
update_quadrature_points | update_JxW_values);
// 获取每个单元上具有的自由度
const unsigned int dofs_per_cell
= fe.n_dofs_per_cell();
// 定义单个单元计算用的全矩阵,而非稀疏矩阵
FullMatrix<double> cell_matrix(dofs_per_cell, dofs_per_cell);
// 定义单个单元计算用的向量
Vector<double> cell_rhs(dofs_per_cell);
// 获取当前单元的局部自由度的全局索引,用于后续进行组装
std::vector<types::global_dof_index> local_dof_indices(dofs_per_cell);
// 遍历所有活动单元
for (const auto &cell : dof_handler.active_cell_iterators())
cell_matrix = 0; // 单元矩阵初始化
cell_rhs = 0; // 单元右手边向量初始化
fe_values.reinit(cell); // 初始化fe_values对象,重新初始化梯度、雅可比行列式等,迭代器cell传入的为单元几何信息
for (const unsigned int q_index : fe_values.quadrature_point_indices())
const double current_coefficient =
coefficient(fe_values.quadrature_point(q_index)); // 计算当前单元上的系数值
for (const unsigned int i : fe_values.dof_indices())
for (const unsigned int j : fe_values.dof_indices())
cell_matrix(i, j) +=
(current_coefficient * // a(x_q)
fe_values.shape_grad(i, q_index) * // grad phi_i(x_q)
fe_values.shape_grad(j, q_index) * // grad phi_j(x_q)
fe_values.JxW(q_index)); // dx
cell_rhs(i) += (1.0 * // f(x)
fe_values.shape_value(i, q_index) * // phi_i(x_q)
fe_values.JxW(q_index)); // dx
最后,将来自
cell_matrix
和
cell_rhs
的贡献转移到全局对象中。
cell->get_dof_indices(local_dof_indices); // 获取单元对应的全局索引
// 自动进行组装,同时为对应于受约束自由度的行和列进行高斯消除
constraints.distribute_local_to_global(
cell_matrix, cell_rhs, local_dof_indices, system_matrix, system_rhs);
现在我们已经完成了线性系统的组装。约束矩阵照顾到了边界条件的应用,也消除了悬挂节点约束。受约束的节点仍然在线性系统中(在矩阵的对角线上有一个非零元素,选择的方式使矩阵具有良好的条件,并且这一行的所有其他条目都被设置为零),但是计算出来的值是无效的(也就是说,
system_rhs
中的相应元素目前没有意义)。我们在
solve
函数的最后为这些节点计算出正确的值。
}
3.7 求解函数
Step6::solve
我们继续逐步改进。解决线性系统的函数再次使用了
SSOR
预处理程序,而且除了我们必须加入悬挂节点约束外,其他的没有改变。如上所述,通过对矩阵的行和列进行特殊处理,从
AffineConstraints
类型的对象中删除了对应于悬挂节点约束和边界值的自由度。这样一来,这些自由度的值在求解线性系统后就有了
错误的、但定义明确的值
。然后我们要做的就是
用约束条件
给它们
分配它们应该有的值
。这个过程被称为
distributing
约束,从无约束的节点的值中计算出受约束节点的值,只需要一个额外的函数调用,你可以在这个函数的结尾找到:
template <int dim>
void Step6<dim>::solve()
SolverControl solver_control(1000, 1e-12); // 设定迭代终止条件
SolverCG<Vector<double>> solver(solver_control); // 将终止条件传递给CG求解器
PreconditionSSOR<SparseMatrix<double>> preconditioner; // 创建SSOR预处理器对象
preconditioner.initialize(system_matrix, 1.2); // 设置松弛因子
solver.solve(system_matrix, solution, system_rhs, preconditioner); // 进行求解
// 从无约束的节点的值中计算出受约束节点的值,通过约束条件进行分配,使所有节点都具有正确的解
constraints.distribute(solution);
3.8 细化网格函数
Step6::refine_grid
我们使用一个复杂的误差估计方案来细化网格,而不是全局细化。我们将使用
KellyErrorEstimator
类,该类实现了拉普拉斯方程的误差估计器;原则上它可以处理可变系数,但我们不会使用这些高级功能,而是使用其最简单的形式,因为我们对定量结果不感兴趣,只对生成局部细化网格的快速方法感兴趣。
尽管Kelly等人推导的误差估计器最初是为拉普拉斯方程开发的,但我们发现它也很适合为一类广泛的问题快速生成局部细化网格。这个误差估计器使用了解在单元面上的 梯度跃变 (这是一个测量二阶导数的方法),并将其 按单元的大小进行缩放 。因此,它是对每个单元的解的 局部平滑性的测量 ,因此可以理解,它对 双曲传输问题 或 波浪方程 也能产生合理的网格,尽管这些网格与专门为该问题定制的方法相比肯定是 次优 的。因此,这个误差估计器可以理解为 测试自适应程序 的一种 快速方法 。
估计器的工作方式是将描述自由度的
DoFHandler
对象和每个自由度的数值向量作为输入,并为网格
triangulation
的每个活动单元计算一个指标值(即
每个活动单元一个数值
)。为此,它需要两个额外的信息:一个是面正交公式,即
dim-1
维物体的正交公式。我们再次使用
3点高斯法则
,这个选择与本程序中的
双二次方有限元形状函数
是一致和合适的。(当然,合适的正交规则取决于误差估计器评估解场的方式。如上所述,梯度的跃变是在每个面上进行积分的,对于本例中使用的二次单元来说,这将是每个面上的二次函数。然而,事实上,它是
梯度跃变的平方
,正如该类文件中所解释的那样,这是一个
二次函数
,对于它来说,
3点高斯公式
就
足够
了,因为它可以
精确地积分5阶以下的多项式
)。
其次,该函数需要一个 边界指标列表 ,用于存储施加 Neumann边界 \partial_n u(x)=h(x) 的位置,以及存储此类边界对应的函数 h(x) 。这些信息通过一个 从边界指标到描述Neumann边界值的函数对象的映射 来表示。在本例程序中,我们不使用Neumann边界值,所以这个映射是空的,实际上是在函数调用期望得到相应函数参数的地方使用映射的默认构造器构造的。
输出是所有活动单元的数值向量。虽然非常 精确 地 计算 解在一个自由度的值是有意义的,但通常 没有必要 特别 精确地计算 一个单元上的解所对应的 误差指标 。因此,我们通常 使用 一个 浮点数 的向量 而不是 一个 双浮点数 的向量来表示误差指标。
template <int dim>
void Step6<dim>::refine_grid()
// 定义存储每个单元误差指标值的数组,使用浮点数据类型,而非双浮点
Vector<float> estimated_error_per_cell(triangulation.n_active_cells());
// 对所有单元的误差指标进行计算
KellyErrorEstimator<dim>::estimate(dof_handler,
QGauss<dim - 1>(fe.degree + 1),
solution,
estimated_error_per_cell);
上述函数为
estimated_error_per_cell
数组中的每个
cell
返回一个误差指标值。现在的细化工作如下:
细化
误差值在
前
30%的的单元,
粗化
那些误差值在
后
3%的单元。
我们可以很容易地验证,如果粗化比例为0,这将导致二维空间中每一步的单元数几乎翻倍,因为细化后单元数为: (1-x)N+4xN=(1+3x)N ,当 x=30\% 时约为两倍。在实践中,通常会产生更多的单元(比两倍稍多),因为 不允许 一个单元被细化两次而相邻的单元却没有被细化;在这种情况下,相邻的单元也会被细化。
在许多应用中 ,被粗化的单元数将被设置为大于3%的数。一个 非零的值 是很有用的,特别是当 初始(粗)网格 由于某种原因已经 相当精细 了。在这种情况下,可能有必要在某些区域进行细化,而在另一些区域进行粗化。在我们这里, 初始网格 是 非常粗糙 的,所以只有在少数可能发生过度细化的区域才有必要进行粗化。因此,一个小的、非零的值在这里是合适的。
下面的函数现在采用这些细化指标,并使用上述方法对网格
triangulation
的一些单元
进行细化或粗化标记
。它来自一个类,该类实现了几种不同的算法,根据单元的误差指标来细化
triangulation
。
// 按照细化指标0.3与粗化指标0.03对网格进行标记
GridRefinement::refine_and_coarsen_fixed_number(triangulation,
estimated_error_per_cell,
0.3,
0.03);
在前一个函数结束后,一些单元被标记为细化,另一些被标记为粗化。然而,细化或粗化本身并没有被立即执行,因为在某些情况下,可能还需要
进一步修改标记
。在这里,我们先不考虑做什么修改,所以我们可以直接告诉
triangulation
按对应的标记进行细化or粗化。
triangulation.execute_coarsening_and_refinement();
3.9 输出结果函数
Step6::output_results
在每个网格的计算结束后,在继续下一个循环的网格细化之前,我们要输出这个循环的结果。
我们已经在
step-1
中看到了如何对网格本身实现这一点。在这里,我们改变一些东西:
-
我们使用两种不同的格式:
gnuplot和VTU。 - 我们在输出文件名中嵌入了循环编号。
-
对于
gnuplot输出,我们设置了一个GridOutFlags::Gnuplot对象,以提供一些额外的可视化参数,使边缘看起来是弯曲的。这将在step-10中进一步详细解释。
template <int dim>
void Step6<dim>::output_results(const unsigned int cycle) const
GridOut grid_out; // 实例化网格输出对象grid_out
// 根据cycle定义对应的输出文件名
std::ofstream output("grid-" + std::to_string(cycle) + ".gnuplot");
GridOutFlags::Gnuplot gnuplot_flags(false, 5);
grid_out.set_flags(gnuplot_flags);
MappingQ<dim> mapping(3);
grid_out.write_gnuplot(triangulation, output, &mapping); // 输出gnuplot格式的结果文件
DataOut<dim> data_out; // 实例化DataOut类对象data_out
// 告诉data_out绑定哪个DoFHandler对象
data_out.attach_dof_handler(dof_handler);
// 告诉data_out解向量是solution变量,以及解在输出文件中的名称"solution"
data_out.add_data_vector(solution, "solution");
// 将数据从前端传输到后端,方便输出各种格式
data_out.build_patches();
// 根据cycle定义对应的输出文件名
std::ofstream output("solution-" + std::to_string(cycle) + ".vtu");
data_out.write_vtu(output); // 输出vtu格式的解
3.10 接口函数
Step6::run
在主函数
main()
之前的最后一个函数仍然是该类的主要驱动,
run()
。它与
step-5
的函数类似,只是在
step-6
程序中再生成一个文件,而不是从磁盘中读取文件,我们自适应地而不是全局地细化网格,并且我们在本函数中输出最终网格的解。
该函数主循环的第一个块是处理网格的生成。如果处于程序块的 第一个循环 ,我们不是像前面的例子那样从磁盘上的文件中读取网格,而是再次使用一个库函数来 创建网格 。域还是一个圆,中心在原点,半径为1(这是函数的两个 隐藏参数 ,有默认值)。
通过观察粗网格,你会注意到它的质量比我们在前面的例子中从文件中读出的网格要差:单元不太均匀。然而,通过使用库函数,这个程序可以在任何空间维度上工作,这在以前是不可能的。
如果我们发现不位于第一个循环,我们就要细化网格。与 上一个例子 程序中采用的 全局细化 不同,我们 现在使用 上述的 自适应程序 。
template <int dim>
void Step6<dim>::run()
// 总共进行八次循环,其中第一次不细化,后面七次都细化
for (unsigned int cycle = 0; cycle < 8; ++cycle)
std::cout << "Cycle " << cycle << ':' << std::endl;
// 如果是第一次循环,则产生一个圆形网格,并全局细化一次
if (cycle == 0)
GridGenerator::hyper_ball(triangulation);
triangulation.refine_global(1);
refine_grid(); // 如果不是第一次循环,则进行局部细化
// 输出活动单元数
std::cout << " Number of active cells: "
<< triangulation.n_active_cells() << std::endl;
setup_system();
// 输出网格的总自由度数
std::cout << " Number of degrees of freedom: " << dof_handler.n_dofs()
<< std::endl;
assemble_system();
solve();
output_results(cycle);
3.11 主函数
主函数的功能与之前的例子相比没有改变,但我们采取了额外的 谨慎措施 。有时,会出现一些问题(比如 写输出文件时磁盘空间不足,试图分配向量或矩阵时内存不足,或者由于某种原因我们无法从文件中读出或写入文件 ),在这些情况下,库会抛出异常。由于这些是 运行时的问题 ,而不是可以一劳永逸的编程错误( 并非逻辑错误 ),这种异常 在优化模式下不会被关闭 ,这与我们用来测试编程错误的 Assert宏不同 。
如果没有被捕获,这些异常会在调用树上传播到主函数,如果在那里也没有被捕获,程序就会被中止。在很多情况下,比如内存或磁盘空间不足,我们什么也做不了,但我们至少可以打印一些文字,试图解释程序失败的原因。下面显示了一种方法。以这种方式编写任何较大的程序都是有用的,你可以通过借鉴这个函数结构来做到这一点。
int main()
这个函数布局的总体思路如下:让我们试着像以前那样运行程序...
try
Step6<2> laplace_problem_2d;
laplace_problem_2d.run();
...如果运行失败了,就要尽量收集尽可能多的信息。具体来说,如果被抛出的异常是一个
派生自C++标准类
exception
的对象,那么我们可以使用
what
成员函数来获得一个字符串,这个字符串描述了异常被抛出的原因。
deal.II
的异常类都是从标准类派生出来的,
exc.what()
函数返回的字符串与使用Assert宏抛出的异常大致相同。在前面的例子中,你已经看到了这种异常的输出,然后你知道它包含了异常发生的文件和行号,以及其他一些信息。这也是下面的语句会打印的内容。
在输出错误信息后,除了以错误代码退出程序外,我们并不能做些其他的(这就是
return 1;
的作用)。
catch (std::exception &exc)
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
如果在某处抛出的异常不是一个从标准异常类派生出来的对象,那么我们根本就不能做任何事情。我们只能简单地打印一个错误信息并退出。
catch (...)
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
如果我们走到这一步,就表示没有任何异常传播到主函数上(可能有异常,但它们在程序或库的某个地方被捕获,不传播至主函数)。因此,程序按照预期执行,我们可以无误返回。
return 0;
4 结果
程序的输出看起来如下:
Cycle 0:
Number of active cells: 20
Number of degrees of freedom: 89
Cycle 1:
Number of active cells: 44
Number of degrees of freedom: 209
Cycle 2:
Number of active cells: 92
Number of degrees of freedom: 449
Cycle 3:
Number of active cells: 200
Number of degrees of freedom: 921
Cycle 4:
Number of active cells: 440
Number of degrees of freedom: 2017
Cycle 5:
Number of active cells: 956
Number of degrees of freedom: 4425
Cycle 6:
Number of active cells: 1916
Number of degrees of freedom: 8993
Cycle 7:
Number of active cells: 3860
Number of degrees of freedom: 18353
正如预期的那样,在每个周期中,单元格的数量大约增加了一倍,自由度数略多于单元数的四倍。
使用
gnuplot
绘制网格图片的命令是:
plot "grid-0.gnuplot" w l
初始网格及其解为:
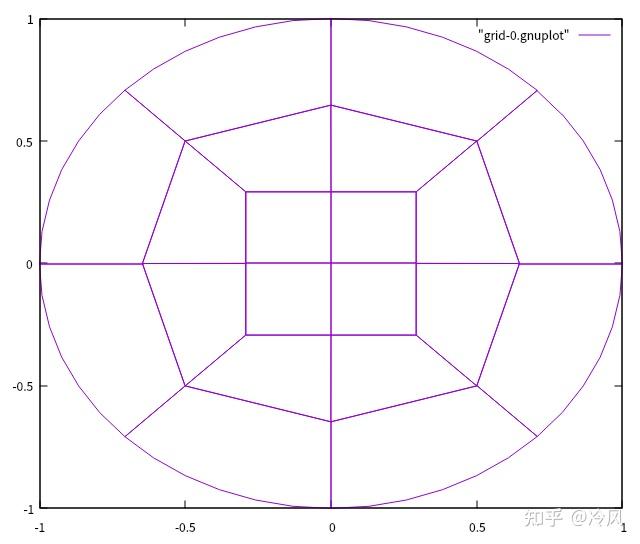
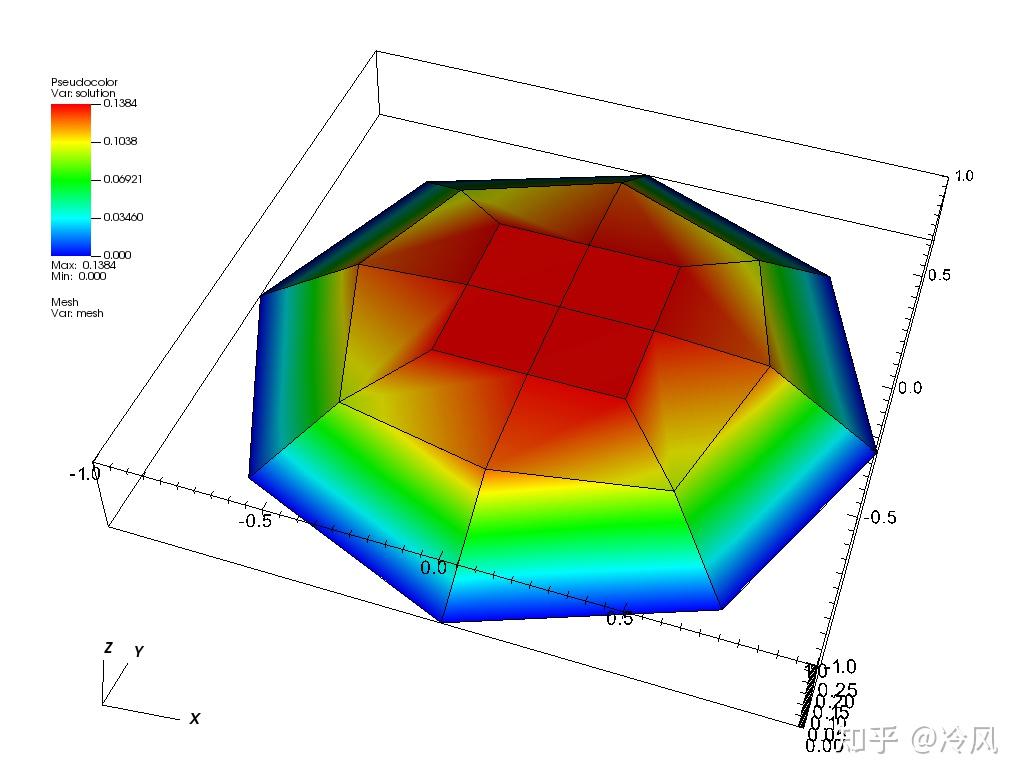
第一次细化后的网格及其解为:
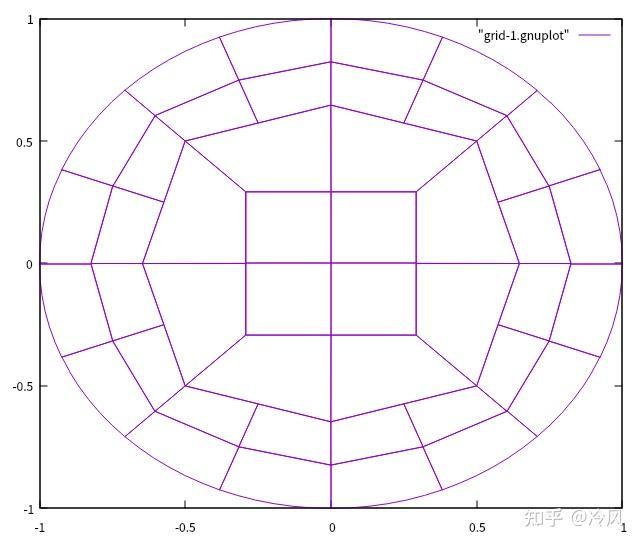
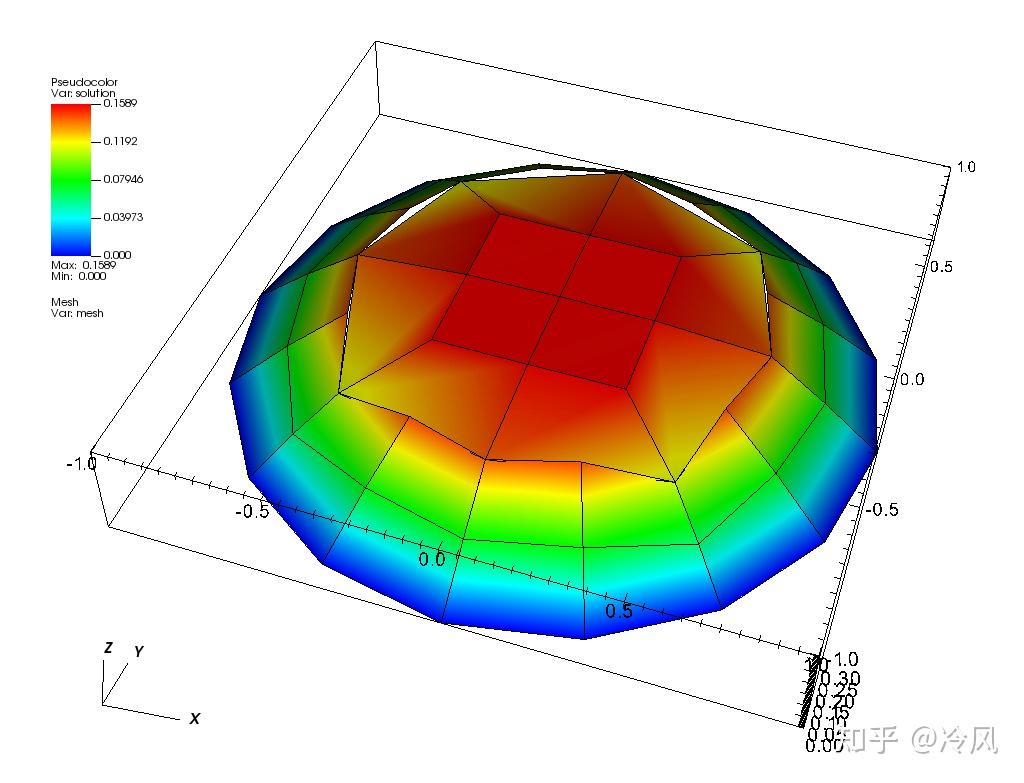
第二次细化后的网格及其解为:
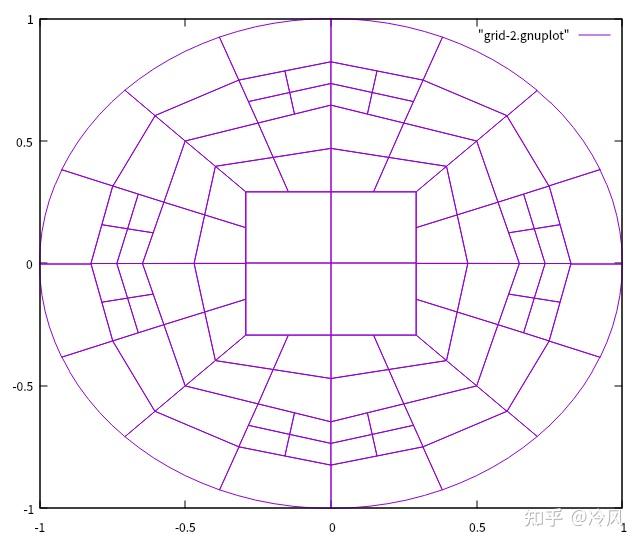
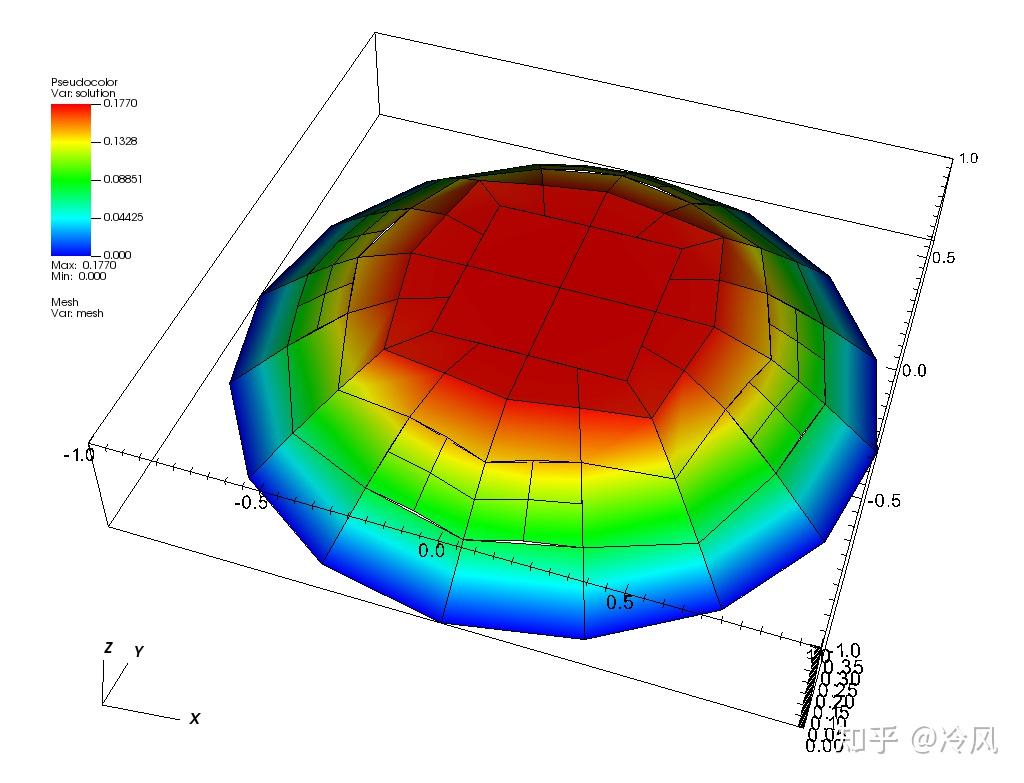
第三次细化后的网格及其解为:
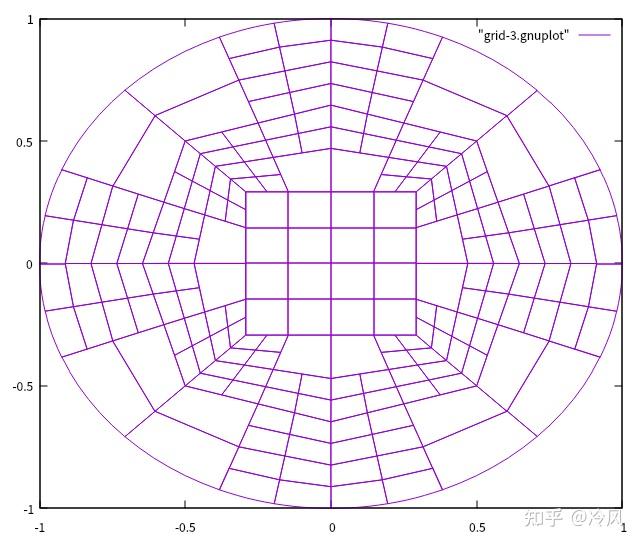
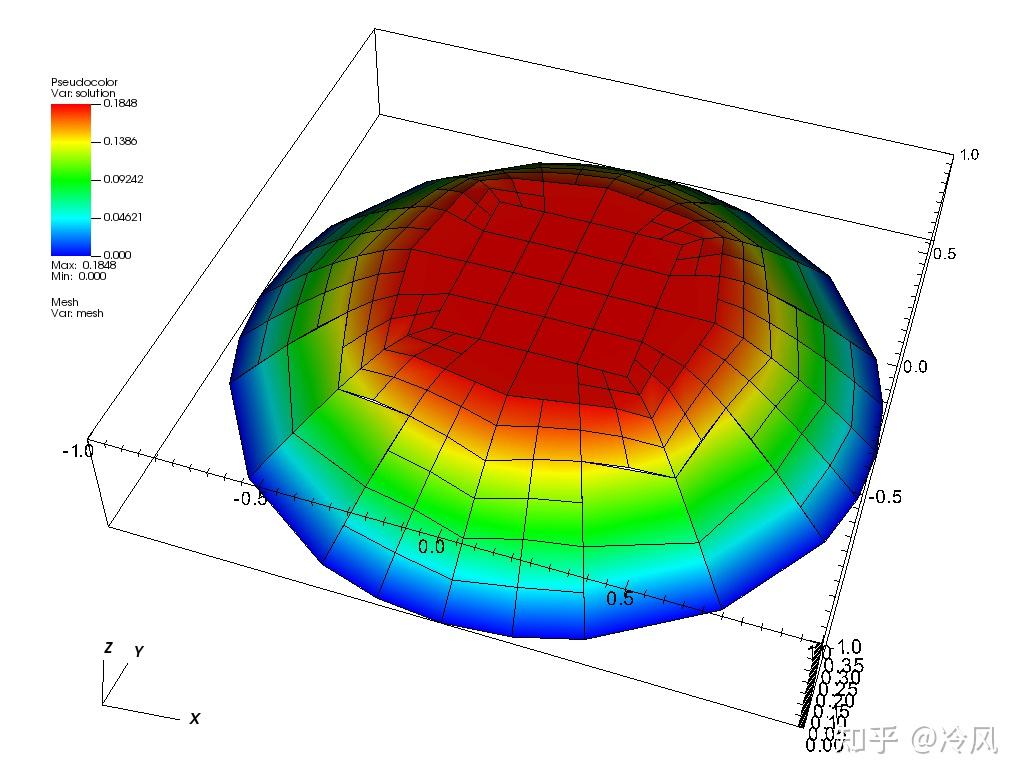
第四次细化后的网格及其解为:
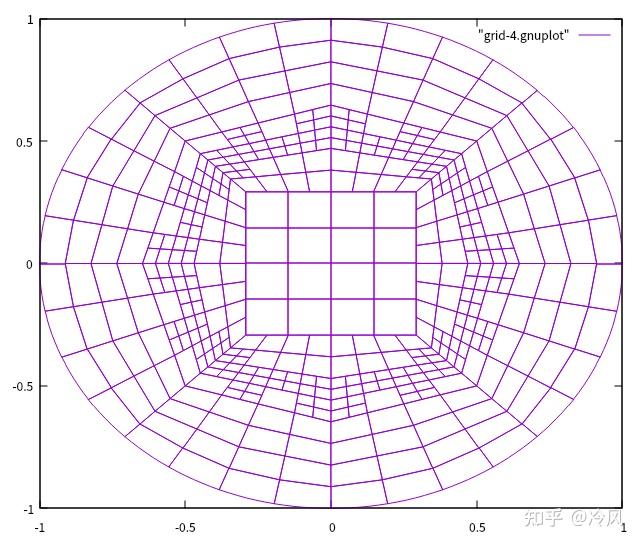
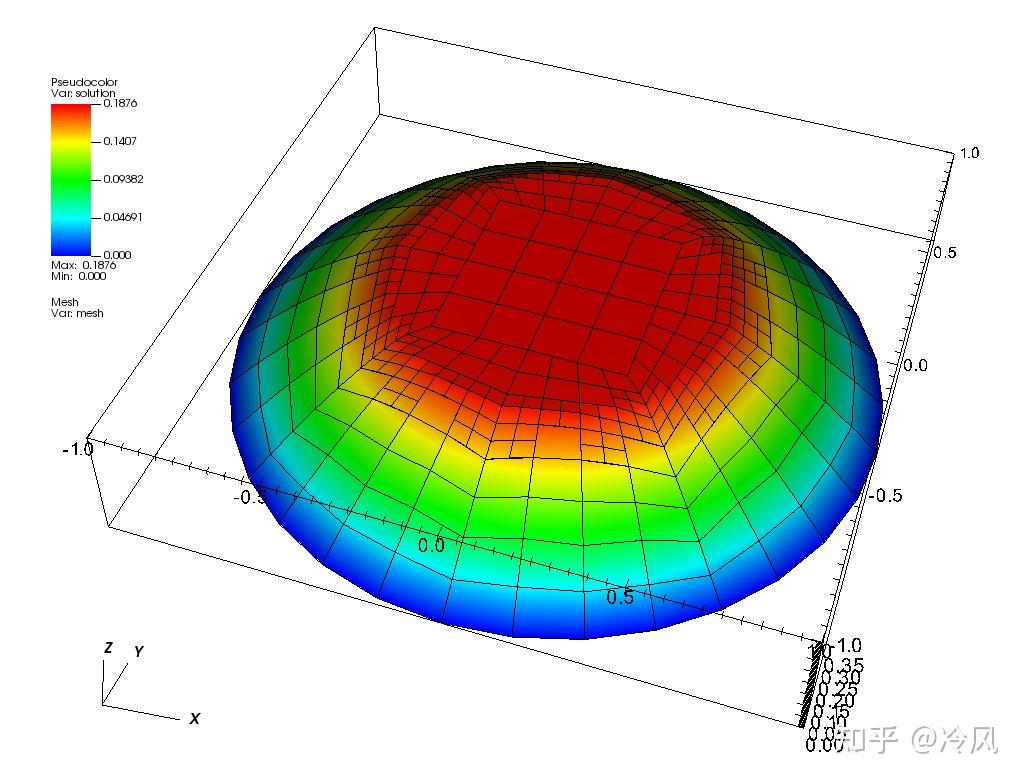
第五次细化后的网格及其解为:
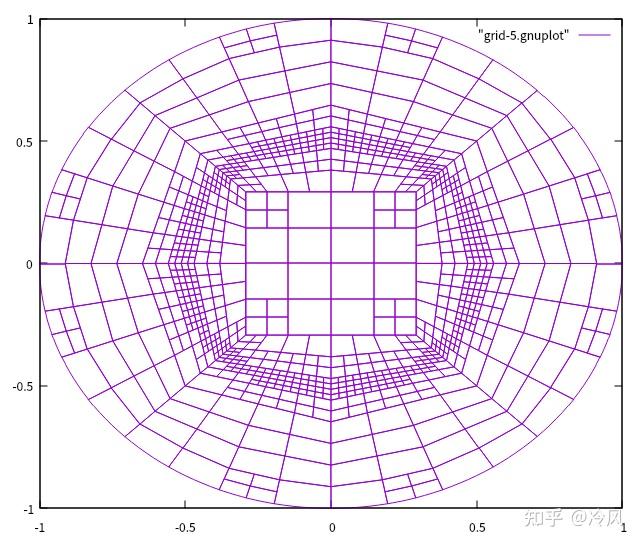
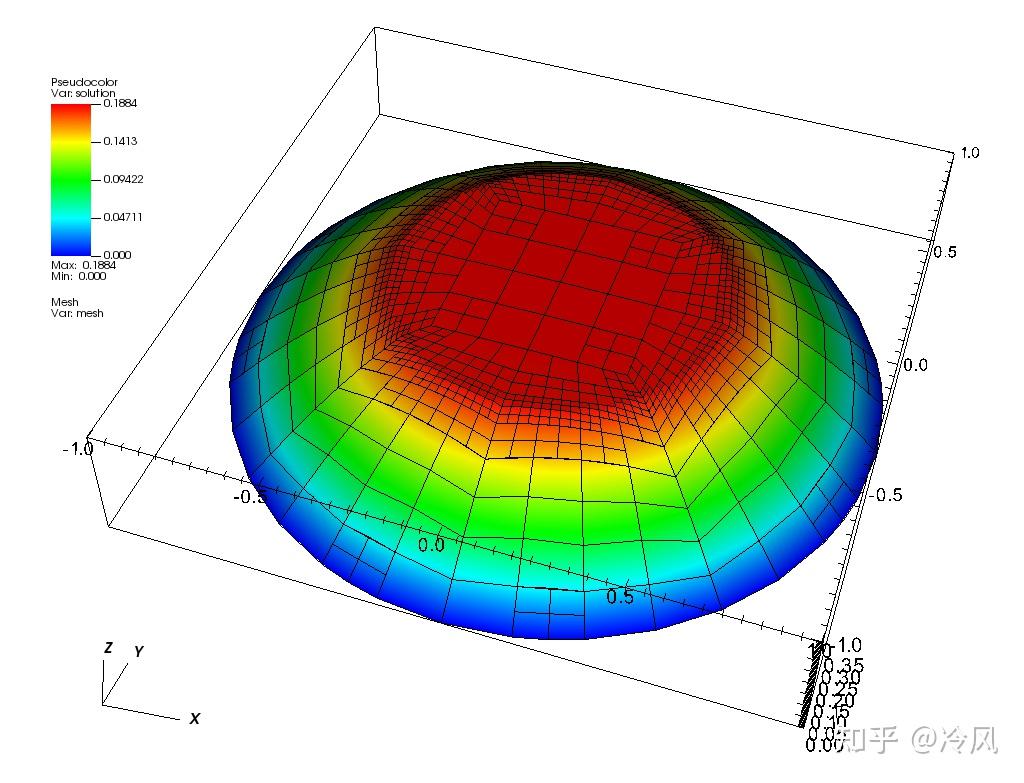
第六次细化后的网格及其解为:
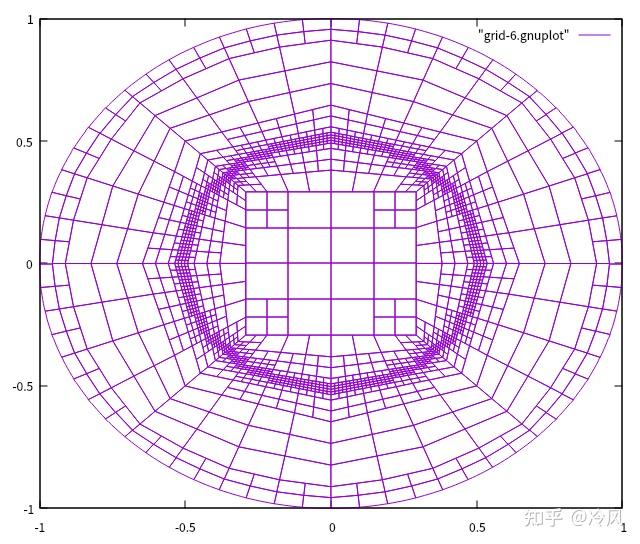

第七次细化后的网格及其解为:
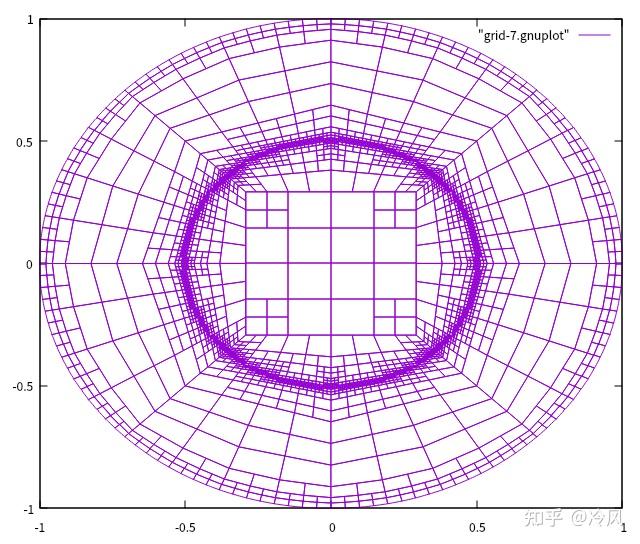
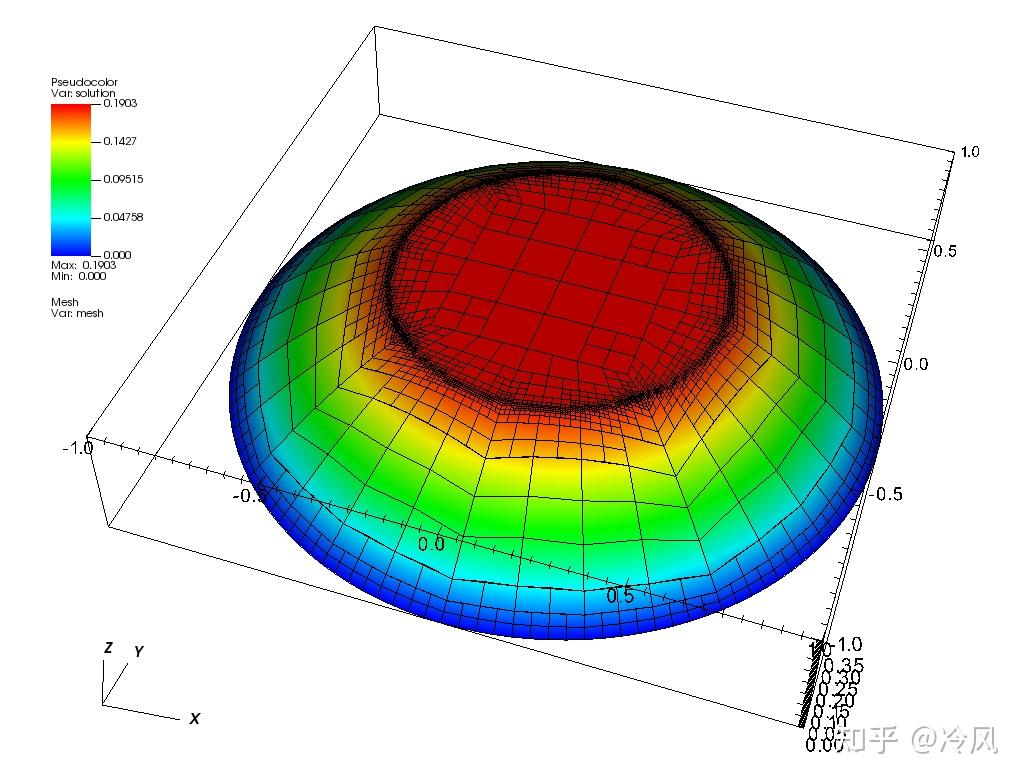
可以清楚地看到,在解有
kink
的区域,也就是离中心半径为0.5处的圆,被细化得最多。此外,解非常光滑和几乎平坦的中心区域几乎完全没有被细化,但这是
由于我们没有考虑到那里的系数很大
的事实(原则上Kelly误差指标可以考虑,但是这个例程中没有考虑)。外面的区域被任意细化,因为那里的二阶导数是恒定的,因此细化主要是
基于单元的大小
和它们
与最佳平方的偏差
。
5 扩展
5.1 求解器和预处理器
如果要解决大规模的问题(比我们这里的问题大得多),有一件事总是值得一试的,那就是尝试不同的求解器或预处理器。在目前的情况下,线性系统是对称的和正定的,这使得CG算法几乎成了求解的典型选择。然而,我们在
solve()
函数中使用的
SSOR
预处理器是有待商榷的。
在deal.II中,改变预处理程序是比较简单的。我们可以尝试
SSOR
的不同松弛因子,把下面的代码:
PreconditionSSOR<SparseMatrix<double>> preconditioner;
preconditioner.initialize(system_matrix, 1.2);
变为:
PreconditionSSOR<SparseMatrix<double>> preconditioner;
preconditioner.initialize(system_matrix, 1.0); // 松弛因子改为1.0
即可。
我们可以使用
Jacobi
作为预处理程序,通过使用:
PreconditionJacobi<SparseMatrix<double>> preconditioner;
Preconditioner.initialize(system_matrix);
我们还可以使用一个简单的
不完全LU分解
,不需要任何阈值处理或加强对角线(为了使用这个预处理程序,你还必须把头文件
deal.II/lac/sparse_ilu.h
加入代码顶部的include列表)。
使用这些不同的前置条件,我们可以比较所需的
CG迭代次数
(通过调用
solver_control.last_step()
获得,在
step-4
已经使用过)以及所需的
CPU时间
(使用
Timer
类),得到以下结果:
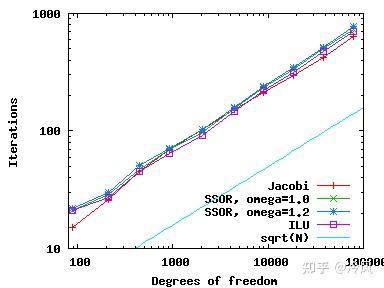
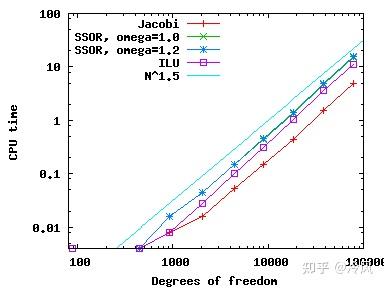
我们可以看到,在这个简单的问题上,所有的预处理程序的表现都差不多,迭代次数增长为 \mathcal{O}(N^{1/2}) ,由于每次迭代都需要 \mathcal{O}(N) 左右的操作,总的CPU时间增长为 \mathcal{O}(N^{3/2}) (对于几个最小的网格,CPU时间小到没有记录)。请注意,尽管它是最简单的方法,但对于这个问题, Jacobi是最快 的。
当有限元
不是
本程序构造函数中设定的
双二次单元
,而是
双线性单元
时,即把
fe(2)
改为
fe(1)
template <int dim>
Step6<dim>::Step6()
: fe(1)
, dof_handler(triangulation)
单元阶数降低后,结果如下:
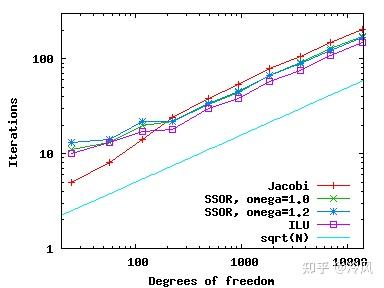
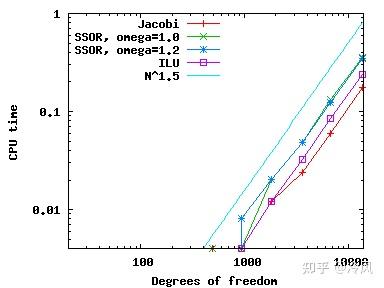
实际上,Jacobi是需要 迭代次数最多 的方法;不过,由于它必须 执行的操作很简单 ,所以它在本问题中仍然是最快的方法。这并不是说Jacobi实际上是一个好的预处理方法——对于 大规模问题 ,它肯定 不是 ,其他方法会好得多——而实际上只是因为它的实现非常简单,可以补偿更多的迭代次数,所以它的速度很快。
从这里得到的信息并不是预处理程序的简单性总是最好的。虽然这对目前的问题可能是正确的,但一旦我们转向更复杂的问题(弹性或斯托克斯,例如
step-8
或
step-22
),就绝对不是这样了。其次,所有这些预处理程序仍然会导致迭代次数随着自由度数
N
的增加而增加,例如
\mathcal{O}(N^\alpha)
;这反过来又会导致总工作量增加为
\mathcal{O}(N^{1+\alpha})
,因为每次迭代需要做
\mathcal{O}(N)
个工作。这种行为是不可取的:我们希望用
\mathcal{O}(N)
次计算来解决有
N
个未知数的线性系统;有一类预处理程序可以实现这一点,即几何(
step-16
、
step-37
、
step-39
)或代数多网格(
step-31
、
step-40
和其他几个)预处理程序。然而,它们要比上述的预处理程序复杂得多。
5.2 获得一个更好的网格
如果你看一下上面的网格,你会发现即使域是单位圆,且系数的跃变是沿着圆的,构成网格的单元也不能很好地跟踪这个几何体。原因在
step-1
中已经暗示过了,在没有其他信息的情况下,
Triangulation
类只看到一堆粗的网格单元,当然不知道它们在一起时可能代表的是什么样的几何形状。出于这个原因,我们需要告诉
Triangulation
在一个单元被细化时应该做什么:
边缘中点和单元中点的新顶点应该位于哪里
,以便子单元比父单元更好地代表示所需的几何图形。
为了直观地了解
Triangulation
对几何体的实际了解,仅仅输出顶点的位置和为每条边画一条直线是不够的;相反,我们必须将内部线和边界线都输出为多段线,使它们看起来是弯曲的。我们可以通过对
output_results
函数的
gnuplot
部分做一个修改来做到这一点。
{
GridOut grid_out;
std::ofstream output("grid-" + std::to_string(cycle) + ".gnuplot");
GridOutFlags::Gnuplot gnuplot_flags(false, 5, /*curved_interior_cells*/true);
grid_out.set_flags(gnuplot_flags);
MappingQ<dim> mapping(3);
grid_out.write_gnuplot(triangulation, output, &mapping);
在上面的代码中,我们已经对位于边界的外表面(即圆的最外圈)做了这个处理,所以我们通过gnuplot绘制出来的
网格外轮廓才是一个圆
!!!:由于我们使用了
GridGenerator::hyper_ball
,它将一个
SphericalManifold
附加到域的边界上,所以会自动进行处理。为了使
网格内部
也能
追踪
到一个
圆形域
,我们需要做一些操作。首先,回顾一下我们的粗网格,它由一个中心的方形单元和周围的四个单元组成:
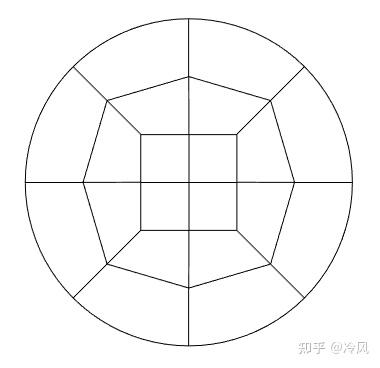
现在我们不只是将
SphericalManifold
对象
连接
到
外部的四个面
,而且还连接到
周边的四个单元以及它们的所有面
。我们可以通过添加下面的代码片段来实现(判断
一个单元的中心到网格中心的距离
是否大于单元直径的一个小倍数,比如说十分之一,这实际上意味着只对网格中心的正方形网格失效)。
GridGenerator::hyper_ball(triangulation);
// after GridGenerator::hyper_ball is called the Triangulation has
// a SphericalManifold with id 0. We can use it again on the interior.
const Point<dim> mesh_center; // 定义一个点对象,用于存放网格中心位置
// 遍历所有活动单元
for (const auto &cell : triangulation.active_cell_iterators())
// 判断点中心到网格中心处的距离是否大于该单元直径的1/10
if (mesh_center.distance (cell->center()) > cell->diameter()/10)
cell->set_all_manifold_ids(0); // 满足条件则设置流形指标为0
triangulation.refine_global(1); // 全局细化一次
经过几次全局细化后,会得到以下类型的网格:
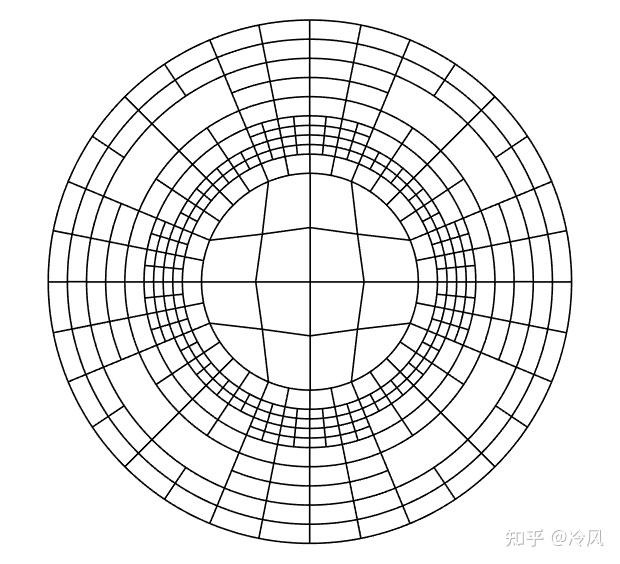
这不是一个好的网格: 中心单元被细化 的方式使得位于原中心单元四个角的子单元 退化 :随着网格细化的继续,它们都 倾向于三角形 。这意味着从 参考单元转换到实际单元 的 Jacobian矩阵 在这些单元中 退化 了,由于 有限元解 的所有 误差估计 都包含 Jacobian矩阵的逆矩阵 ,你将在这些单元上得到 非常大的误差 ,并且随着网格细化的程度提高,收敛阶数也会越来越低,因为这些角落的单元在网格细化中变得越来越差。
所以我们需要更聪明的东西。为此,考虑以下最初由Konstantin Ladutenko开发的解决方案。我们将使用以下代码:
GridGenerator::hyper_ball(triangulation);
const Point<dim> mesh_center; // 定义一个点对象,用于存放网格中心位置
const double core_radius = 1.0/5.0, // 定义中心单元的半径
inner_radius = 1.0/3.0; // 定义内部单元的半径
// 中心单元:即粗网格中心的四个正方形,它们不能被细化
// 内部单元:中心四个正方形加上周围一圈单元
// Step 1: 收缩内部单元
// 由于上面提到的退化问题,我们不能从内单元中得到一个圆。
// 相反,我们应该将内单元缩小到中心半径为1/5的地方
// 选择的这个半径1/5原因是:要远离系数会出现不连续的地方(即半径为1/2处)
// 而且我们要让单元界面真正位于一个圆上。
// 由于圆心刚好是坐标系的原点,我们可以通过缩放每个顶点的位置来实现这种收缩。
// 遍历所有活动单元
for (const auto &cell : triangulation.active_cell_iterators())
// 判断单元中心到网格中心的距离是否小于1e-5
if (mesh_center.distance(cell->center()) < 1e-5)
// 若成立,则遍历该单元的所有顶点(实际上只有中间的几个正方形网格满足)
for (const auto v : cell->vertex_indices())
// 进行收缩:顶点坐标乘以core_radius再除以顶点坐标到网格中心的距离
cell->vertex(v) *= core_radius/mesh_center.distance(cell->vertex(v));
// Step 2: 细化除中心单元外的所有单元
// 遍历所有活动单元
for (const auto &cell : triangulation.active_cell_iterators())
// 判断单元中心到网格中心的距离是否大于等于1e-5(实际上只有中间的几个正方形网格不满足)
if (mesh_center.distance(cell->center()) >= 1e-5)
cell->set_refine_flag(); // 若成立,则标记需要进行细化
triangulation.execute_coarsening_and_refinement(); // 进行细化或粗化
// Step 3: 调整外部单元的内部子单元的大小
// 上一步中用四个子单元替换了每一个外层单元,
// 但现在相交的径向距离并不是我们后续细化步骤想要的。
// 因此,将刚刚创建的顶点沿着径向方向移动到我们需要的地方。
// 遍历每个活动单元
for (const auto &cell : triangulation.active_cell_iterators())
// 遍历单元的所有顶点
for (const auto v : cell->vertex_indices())
// 定义距离变量 dist 等于顶点到网格中心的距离
const double dist = mesh_center.distance(cell->vertex(v));
// 判断 dist 是否大于1.001倍的中心半径且小于0.9999(即:不包含网格外轮廓,也不包含中心半径上的顶点,只在这个环形区域内取)
if (dist > core_radius*1.0001 && dist < 0.9999)
// 若满足条件,则将顶点坐标乘以内半径再除以顶点到网格中心的距离(即:缩放)
cell->vertex(v) *= inner_radius/dist;
// Step 4: Apply curved manifold description 应用弯曲流形的描述
// 如上所述,我们不能指望将内部的四个单元(或其面)细分为同心圆,
// 但我们可以对位于内部半径之外的所有其他单元进行细分。
// 为此,我们在所有单元格上循环,并确定它是否在这个区域内。
// 如果不在,那么我们将该单元及其所有边界面的流形描述设置为
// 上面已经介绍过的描述球形流形的流形,该流形将用于后续的网格细化。
// 遍历所有活动单元
for (const auto &cell : triangulation.active_cell_iterators())
// 定义bool类型变量,作为是否处于内部半径之内的标志
bool is_in_inner_circle = false;
// 遍历单元上所有顶点
for (const auto v : cell->vertex_indices())
// 如果顶点到网格中心的距离小于内部半径
if (mesh_center.distance(cell->vertex(v)) < inner_radius)
is_in_inner_circle = true; // 标志为真,退出循环
break;
