[RL] CS285/294: Lecture 8 DQN

lec7 讲了Q-learning，lec8的目标是能在实践中使用Q-learning，因此进一步讲Deep RL with Q-function。

今天的主要内容如下：

1. 在Q-learning中使用深度网络
2. 一个更普遍意义的Q-learning 算法 - DQN
3. 实际中提升Q-learning的算法-DDQN
4. 连续动作空间的Q-learning 方法

online Q-learning的问题

在Lecture 7中我们主要介绍了Q-learning，其实就是只使用critic的actor-critic算法，然后取最合适的动作a。但是Q-learning 尤其是online Q-learning 存在两个问题：

1. Q-network 不收敛

在online Q iteration 算法中的第三步，似乎是一个梯度下降的迭代方式，按理说如果是梯度下降只要参数学习率设置合理，总能找到一个局部最优解。但online Q-learning 并不能保证收敛，为什么呢？原因是：

Q-learning的更新方式并不是梯度下降，即使形式上看着像。 我们在说梯度下降时，往往指label是固定的，但是其实这里的 y_i 每次都在变化。当我们的目标是在游走的时候，模型肯定就不会收敛，这也说其实不是梯度下降的原因。

2. online收集的transition数据并不是相互独立的

假设这条曲线是样本的全过程，而online跟新，每次我们都只收集相邻的四个，因此非常容易局部拟合而忽略全局状态。解决这个问题当然可以用actor-critic中的想法，并行跑多个worker：

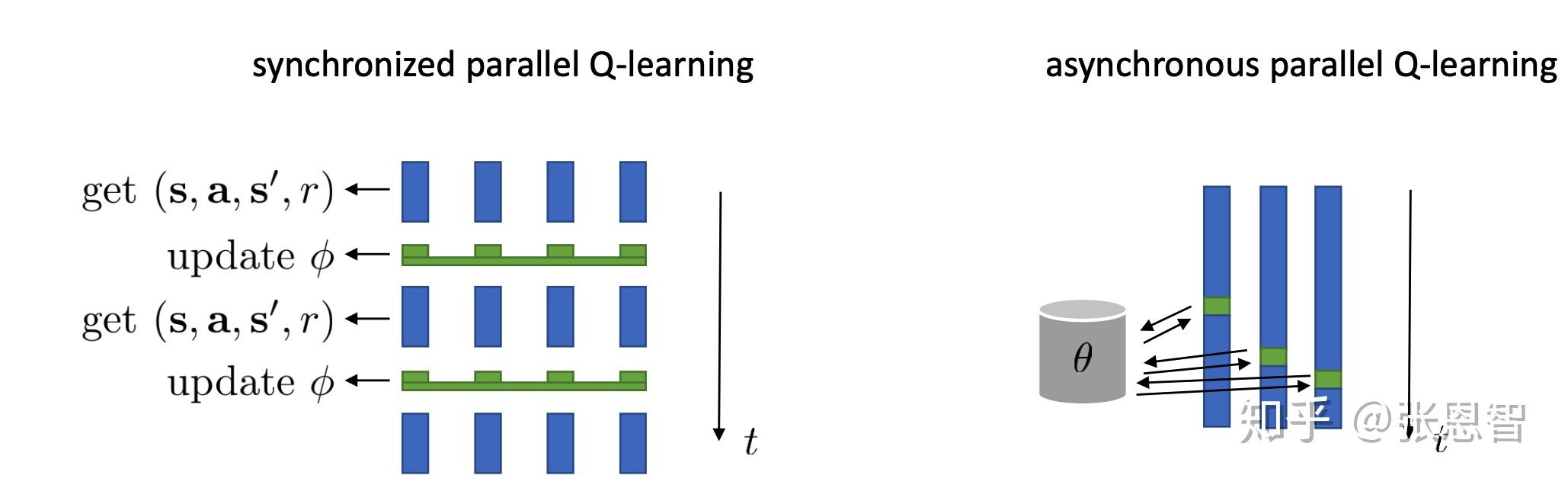
2.如何解决这两个问题？

首先第二个问题，样本不独立的问题，除了使用并行也很好解决，思路是这样的：

2.1 Replay buffer

我们建立一个buffer，每次从其中随机的取样本进行更新Q-network，这样就能保证（我觉得这样online就变成offline了）：

1. 随机保证样本独立
2. 多样本保证策略梯度稳定

当然为了保持Q-learning的性能，需要不断向buffer中添加新的转移样本，添加的方法可以来自我们当前的Q-learning的policy也可以是其他的policy：

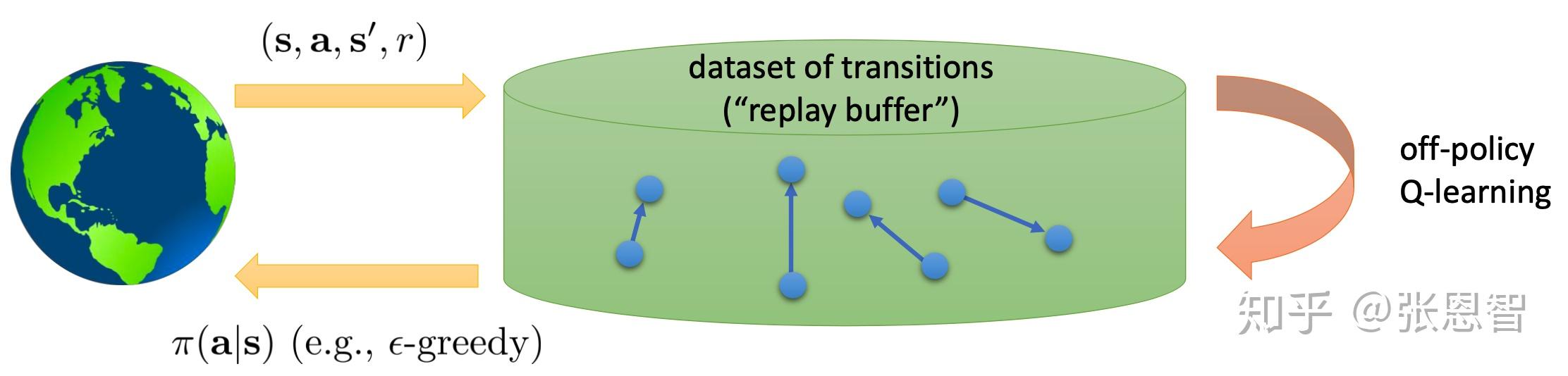
将产生buffer与更新放在一起，就得到了新的算法，叫Q-learning with replay buffer：

对于第一个，lable漂移导致不收敛问题，解决思路如下：

2.2 Target net & Deep Q-learning

不收敛是因为，使用一步梯度并且目标转移，那么我们重新等一下，仿照如下：

我们定义第三步更新是取得全局最优的Q，因此此时Q其实是fix-point在Q-net上的投影，因为最优所以稳定（每次更新都是自己），而 本质上Deep Q-learning之所以收敛是因为深度网络很好的拟合了Qvalue导致fix-point就在或者非常靠近深度网络上 ，虽然我不禁疑问如何保证取到全局最优？还不是梯度下降？但是这给了我们思路是，让 y_i 保持不变，或者一定程度的不变，是更新稳定的必要条件，因此我们引入一个target-net的概念：

target-net 其实就是旧模型，当前模型的更新被旧模型约束，每隔N次大的更新一下旧模型，这样就能保证在更新当前模型时，label都是固定的，这样就稳定了。其实经典的deep Q-learning 算法就是在 K 取值为1下的情景：

2.3 一些小的改进

N次更新旧网络会有一个延迟问题：

比如你让N取5，那么第一次的 Q_{\phi} 和第五次的 Q_{\phi} 其实差别已经很大，而 Q_{\phi^{\prime}} 却没变，这有些不公平，有一个改进策略是线性分割一下：

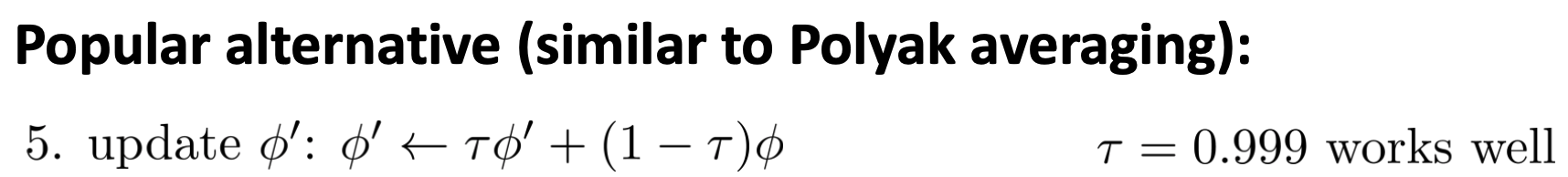
2.4 泛Q-learning(general view of Q-learning)

总体而言Q-learning分三个部分，可以用三个进程来并行描述：

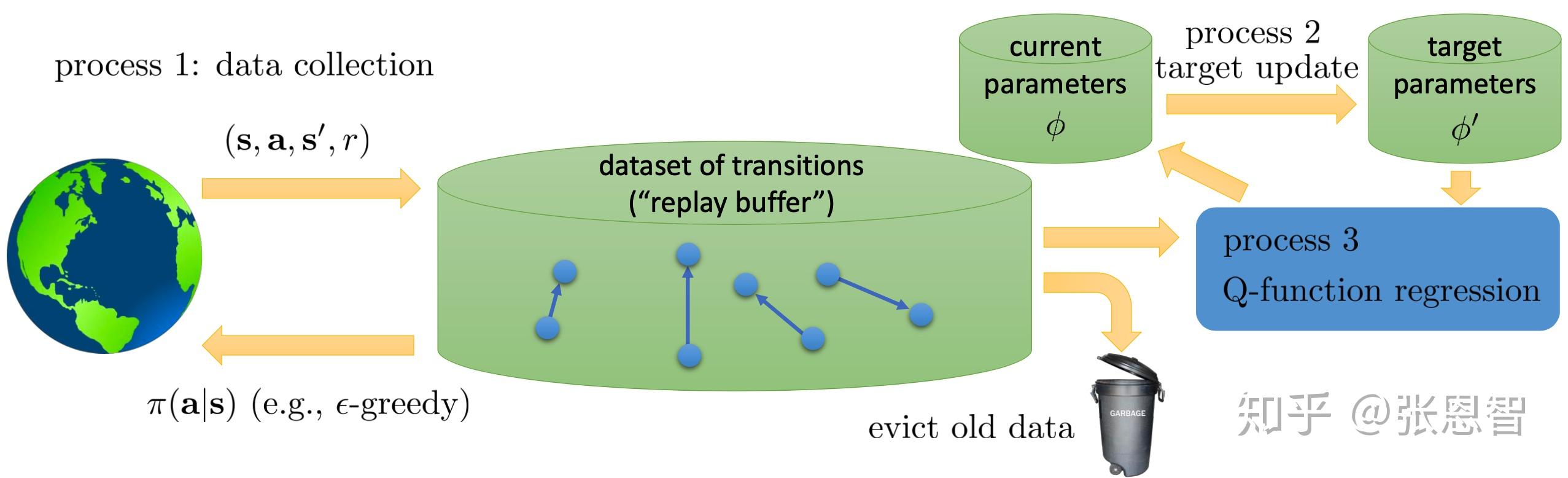
分别是采集数据，更新当前网络（K），更新target-net（N），目前说的的Q-learning只是在这N和K的取值和采集数据的速度上有所不同，或者嵌套不同，比如：

• online Q-learning：这三个速度保持一致，都是1。
• DQN：收集数据和更新当前网络速度一致，进程2比较慢
• Fitted Q-iteration：非并行，1套着2，2套着3（套着==loop）

3.Q-learning 的改进

如果要改进Q-learning，首相要问Q-net是否准确？

3.1 Q-net 是否估计的准确？

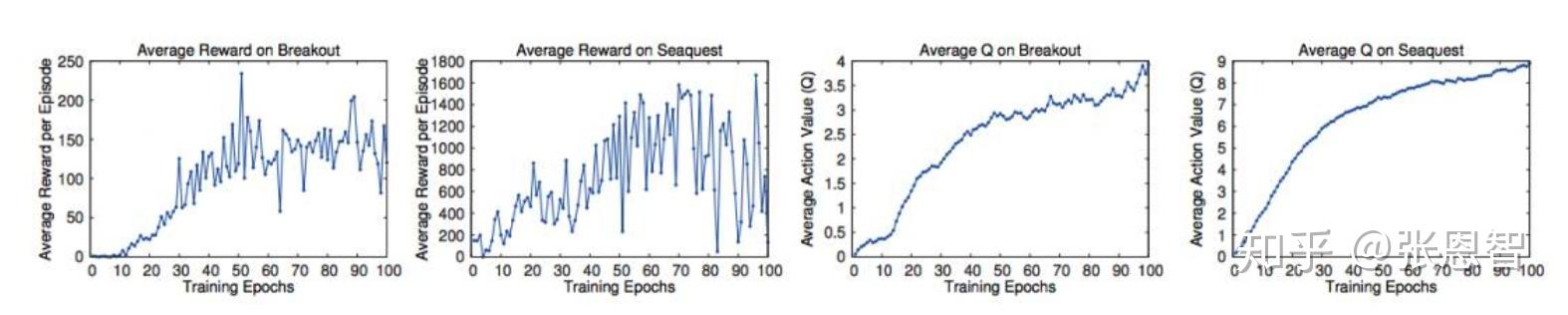
这4张图是Atari的两个游戏，左边2张是真实奖励，右边2张是估计奖励，从趋势上来看至少吻合。但是：

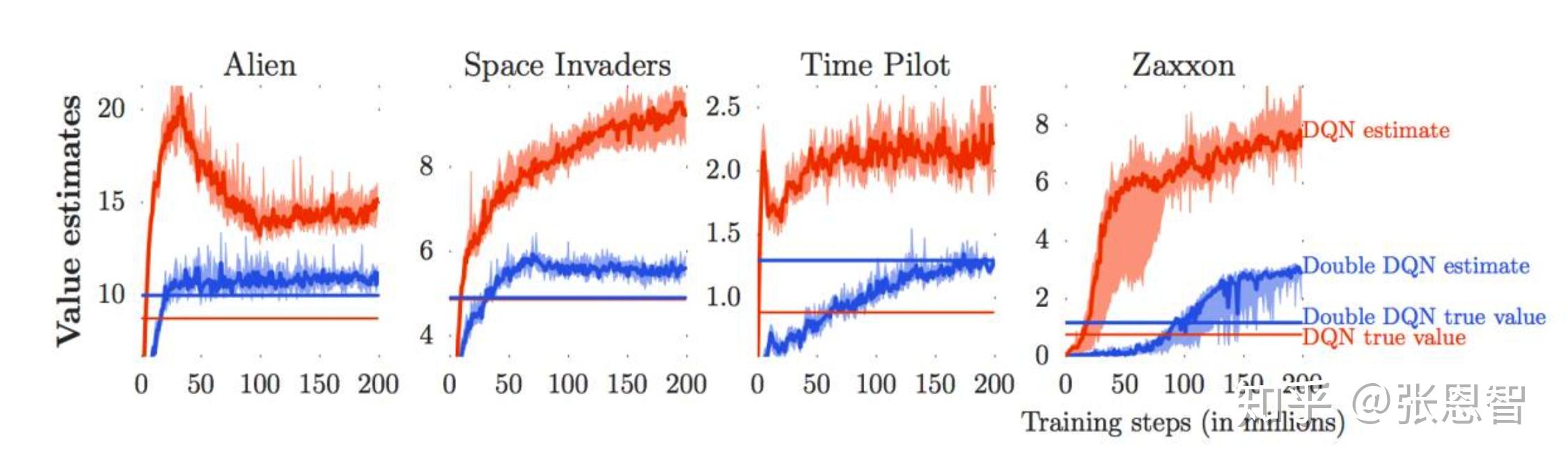
这是四个atari游戏，我们只看红色的线，红色的曲线是Q-net估计的奖励，红色直线是实际的奖励。我们可以看到，Q-net的估计值总是比实际值高很多，这是为什么呢？

3.2 Q-net 高估的一个解释

如果 X_1 和 X_2 是两个随机变量，则有：

E[max(X_1,X_2)]\geq max(E[X_1],E[X_2])

这个说明什么呢？对随机变量先取max会导致均值上移，这就是Q-net变高的直觉解释。

每次Q-net的迭代都是对Q-net在 s 下取使其最大的 a ，而在 s 下的Q-net本身是一个非常崎岖不平的曲线，对其取max无疑会选择过估计的那个动作 a ，并且一次一次的迭代，每次取最大max，我估计Q-net的指也很像是单调递增了。

解决的办法就是double deep Q-learning（DDQN）

3.3 double deep Q learning

DDQN的核心想法是，既然对于同一个网络Q，取action导致误差的value，那么我们干脆把取action和评估reward交给两个net来做。一个提供动作，一个评估Q-value。这样的好处是，选择相对较优的action，同时不因noise的原因，推升value。具体更新方法如下：

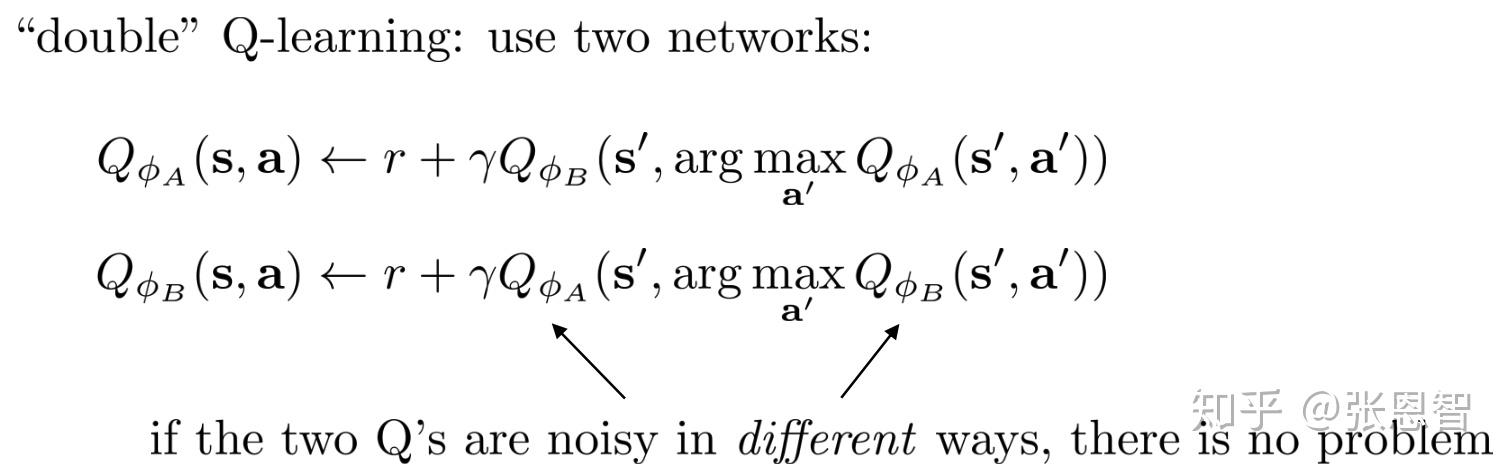
在更新 \phi_A 的时候，通过计算 \phi_A 的argmax来取得action， \phi_{B} 用来评估value。同理，在更新 \phi_B 时，通过计算 \phi_B 的argmax来取得action，而用 \phi_A 来评估value。这样只要两个网络的误差不一致，那么就可以降低DQN的过高估计问题。

in practice

实际使用的时候，只要将我们当前的网络叫做 \phi_A ，target-net叫做 \phi_B ，然后在评估value的时候用 \phi_B 就可以了，如下：

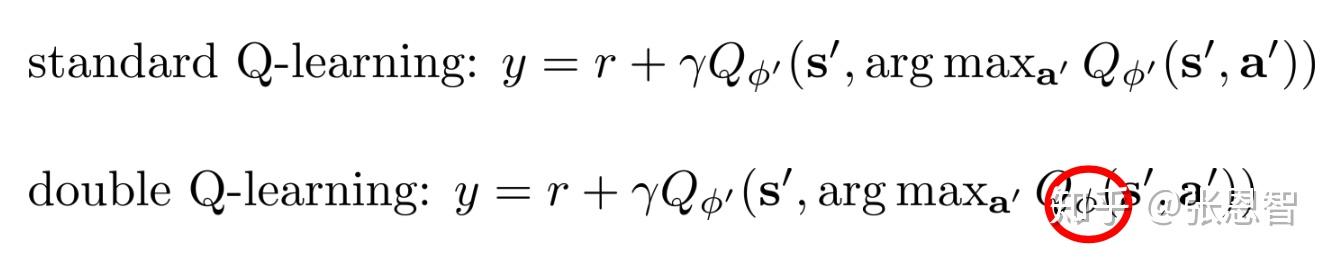
这样感觉还是一个网络结构，参数不一样罢了， 其实说白了 \phi_B 起到了一个稳定器的作用，防止因为argmax导致的误差产生的bias。

3.3 Muti-step returns

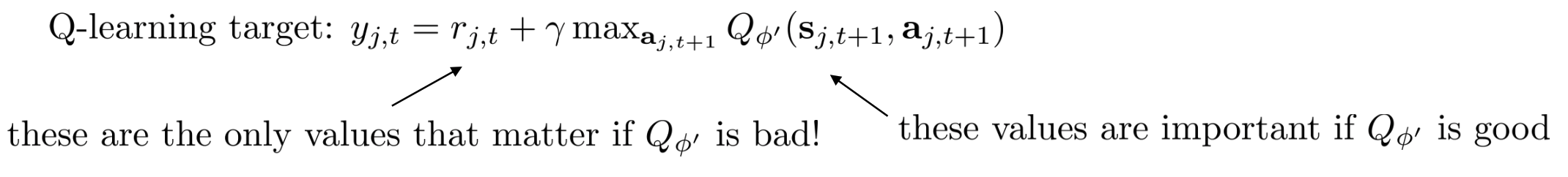
再回到我们的Q-learning 的target，target的label由两部分组成，第一部分是当前的奖励，第二部分是Q-net 估计的奖励。我们来问一个问题： 如果Q-net估计的不太准咋办？

如果Q-net估计的不太准，我们应该更关注第一项的准确度，而把第二项推后，如下式子：

这个target label 分为两个部分，第一部分是N步的真实奖励，第二部分是N步之后的Q估计奖励。这样做的好处是：

1. 当Q-net估计不太准的时候，bias更小。因为我们降低了Q-value的权值，而提高了真实奖励的权值。
2. 更快。

缺点是，保持正确性需要onpolicy。为什么？因为我们需要知道N次的转移概率，而不只是一次的transition。怎么改善这一点呢？

• 无视。往往效果挺好
• 只选择由N步数据的transition
• 重要性采样

4. Q-learning对于连续的动作

当动作是连续的会有哪些问题：

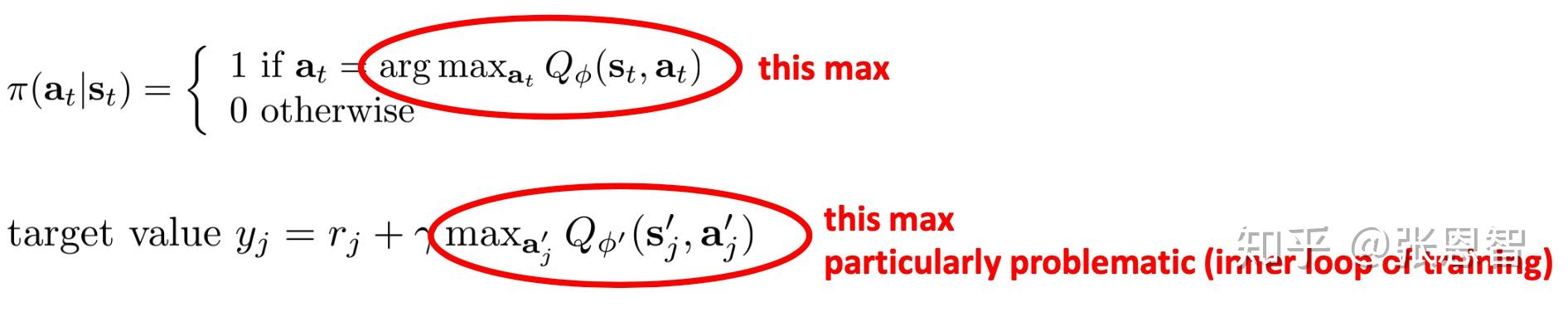
不好选择动作，因为动作无穷个。解决的方法通常有三种。

4.1 Random sampling

就是均匀离散化，然后假设采样最大值就是全局最大值。好处是可并行，快。坏处是不非常准确。但是可以重采样，提升精度，比如CEM(cross-entropy method)

4.2 easily optimized Q-function

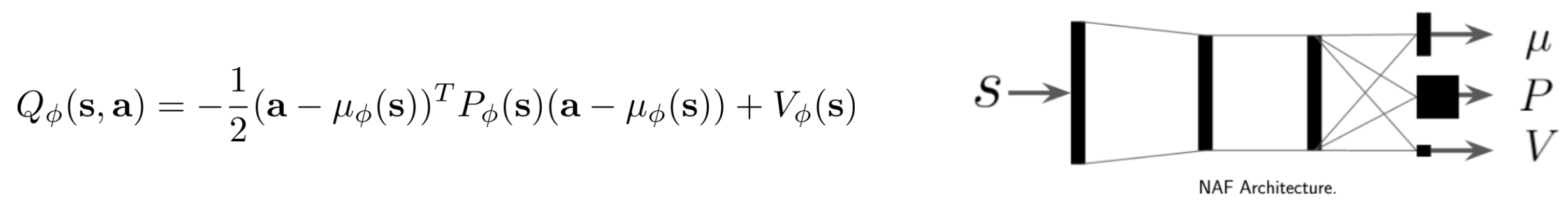
这类想法是，重新构筑一个很好优化Q-function，比如这里提到的NAF(normalized advantage function)。因为，其实此处 \mu_{\phi} 就是大体最优的策略（忽略u估计不准的情况...）所以不用太多的改变算法的同时，效率和Q-net差不多，坏处是，降低了网络的表征能力（这也是经验所得）。

4.3 Approximate maximizer

这里有一篇论文主要是这个方法，DDPG (Lillicrap et al., ICLR 2016) 。想法其实不复杂，就是使用一个代理网络，根据状态评估最佳的action。因此又引入一个network，所以此时如果算是target-net（DDQN），和这个代理网络就有三个网络，降低了推理效率，但提高了policy的效率。

更新方法也是向后传递，给出完整的DDPG

以上就是lec8的大体内容，包括DQN和DDQN，以及一些改进方法。