算法从入门到“放弃”(10)- 堆排序
本系列文章
排序系列
本文提炼
堆排序算法,是一种不稳定的基于比较的排序算法。
什么是堆排序?
定义来自于 维基百科,堆排序,Heap Sort.
在计算机科学中,堆排序是一种基于比较的排序算法。堆排序可以被认为是一种改进的选择排序:就像选择算法一样,它将输入分成已排序的和还未排序的区域,它通过提取未排序的区域内最大的元素并将其移动到已排序的区域来迭代缩小未排序的区域。堆排序相对选择排序改进的部分包括使用堆数据结构而不是线性时间的搜索来找到最大值。
虽然在大多数机器上的实际运行速度要比实现良好的快速排序慢一些,但是它的最坏时间复杂度是 O(n *log(n))。堆排序是一种就地in-place 排序算法,而且它不是稳定排序。
堆排序Heapsort 是J. W. J. Williams在1964年发明的。这也是堆诞生的时候,Williams 将其本身作为一个有用的数据结构提出。同年,R. W. Floyd发表了一个改进的版本,可以对数组进行就地排序,继续他早期对 treesort 算法的研究。
我自己的看法
堆排序,就是利用堆的特征来对目标输入数组进行排序;依据目的是从大到小还是从小到大,我们可以相应地用最大堆排序或则最小堆排序来取出堆顶的最大数或最小数,再将剩下的堆调整为最大堆或最小堆;整个过程持续迭代至只有一个数剩下。
什么是堆?
这个问题本应该在我的数据结构系列里进行讲解,奈何算法系列先行一步讲到了堆。那我们先来简单聊聊,等到日后我更新数据系列到了堆再来进行补充。
讲解堆之前,我们先了解下什么是树形结构,下面的树结构 tree structure 引用自 维基百科 。
树状结构或树形图是一种表示图形形式结构的层次结构的方法。它被命名为“树状结构”,因为其经典的表示类似于一棵树,尽管与实际的树相比,图表通常是颠倒的,顶部是“根”,底部是“叶子”。
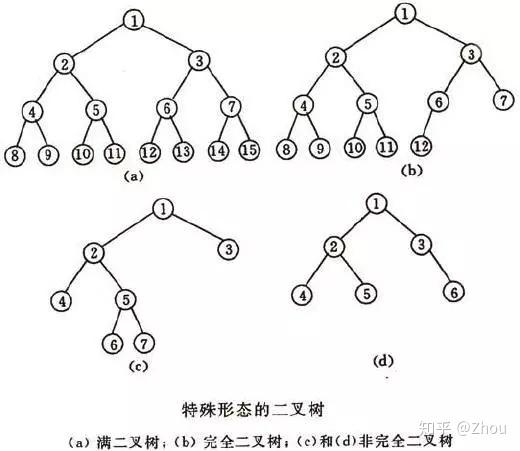
而在树结构中,又有一个大名鼎鼎的二叉树binary tree 结构。什么是二叉树呢?简单来说,二叉树结构指的是该树每个节点最多有两个子树的树结构,左边的子树称为左子树,右边的称为右子树,次序不能颠倒;特征是第i 层至多有2^(i-1) 个结点;深度为k 的二叉树至多有2^k-1 个结点。
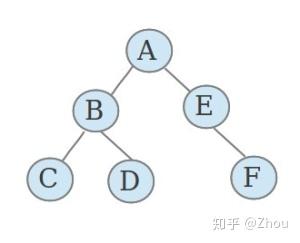
二叉树又可以被分为满二叉树 full binary tree(一棵深度为 k,且最底层有 2^(k- 1) 个节点称之为满二叉树;形如其名,所有的节点都是满的)和完全二叉树 complete binary tree(深度为 k,有 n 个节点的二叉树,当且仅当其每一个节点都与深度为 k 的满二叉树中序号为 1 至 n 的节点对应;简单来说,就是除深度是k 层之外,其他各层(1至k-1)的节点数都达到最大个数,第k 层的所有节点都连续几个在最左边)。
那么重点终于在基本介绍完树形结构后来了,什么是堆呢?
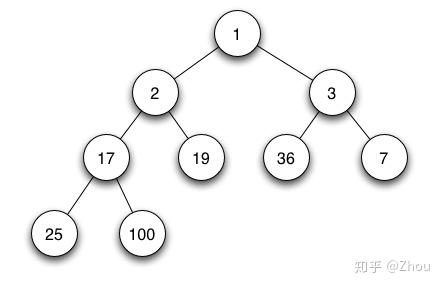
在计算机科学中,堆是专门的树型数据结构。堆的属性有:如果P 是C 的父节点,那么P 的关键(P 的值)就大于或等于(在最大堆排序) 或 小于或等于(在最小堆排序)C 的关键。堆在堆的最“顶部”(没有父节点)的节点称为根节点。
引用自 维基百科
通俗来说,堆可以被看作是一棵树的数组对象,堆中某个节点的值总是不大于或不小于其父节点的值。
堆的实现通常是通过构造二叉堆实现。而且因为二叉堆的应用很普遍,当不加限定时,堆通常指的就是二叉堆。
堆(二叉堆)可以视为一棵完全的二叉树。完全二叉树的一个优秀的性质就是,除了最底层之外,每一层都是满的,这使得堆可以利用数组来表示(一般的二叉树通常用链表作为基本容器表示),每一个结点对应数组中的一个元素。
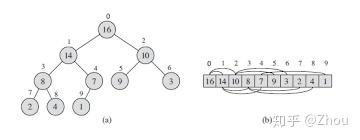
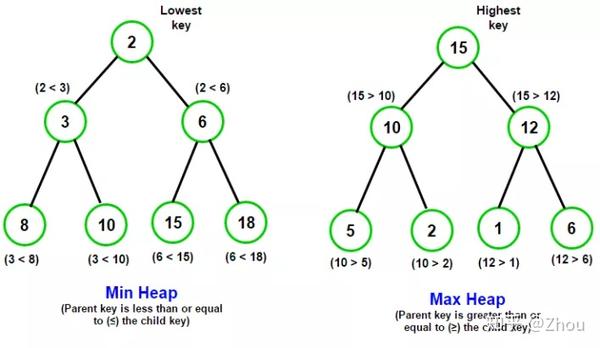
而二叉堆一般分为两种:最大堆和最小堆。
最大堆:最大堆中的最大元素在根结点(堆顶);堆中每个父节点的元素值都大于等于其子结点(如果子节点存在)
最小堆:最小堆中的最小元素出现在根结点(堆顶);堆中每个父节点的元素值都小于等于其子结点(如果子节点存在)
堆的介绍就先到,言归正传,我们看堆排序的基本思想。
基本思想
输入 :一系列的无序元素(比如说,数字)组成的输入数组A
经过 :堆排序的过程可以具体分为三步,创建堆,调整堆,堆排序。
创建堆,以数组的形式将堆中所有的数据重新排序,使其成为最大堆/最小堆。
调整堆,调整过程需要保证堆序性质:在一个二叉堆中任意父节点大于其子节点。
堆排序,取出位于堆顶的第一个数据(最大堆则为最大数,最小堆则为最小数),放入输出数组B 中,再将剩下的对作调整堆的迭代/重复运算直至输入数组 A中只剩下最后一个元素。
输出 :输出数组B,里面包含的元素都是A 中的但是已经按照要求排好了顺序
图解

评价算法好坏
堆排序是非稳定的排序算法
分类:排序算法
数据结构:数组
最优时间复杂度:O(n*log(n)),当keys 的值都不一样;O(n),当keys 的值都一样
最坏时间复杂度:O(n*log(n))
平均时间复杂度:O(n*log(n))
最坏空间复杂度:辅助O(1)
实例分析
本文实例引用自 数据结构示例——堆排序过程 ,侵权删。
假设我们要对目标数组A {57, 40, 38, 11, 13, 34, 48, 75, 6, 19, 9, 7}进行堆排序。
首先第一步和第二步,创建堆,这里我们用最大堆;创建过程中,保证调整堆的特性。从最后一个分支的节点开始进行调整为最大堆。
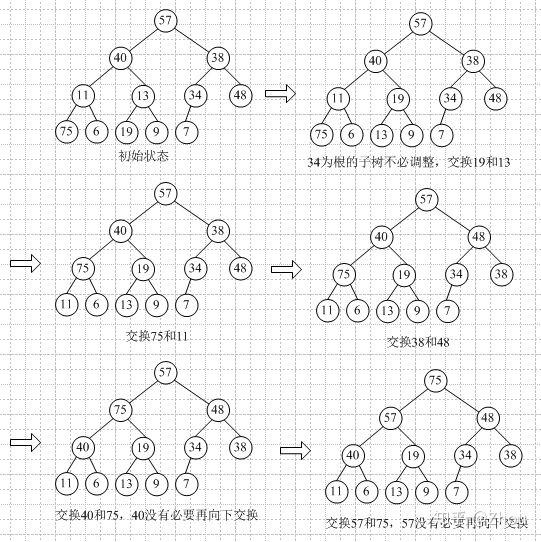
现在得到的最大堆的存储结构如下:

接着,最后一步,堆排序,进行(n-1)次循环。
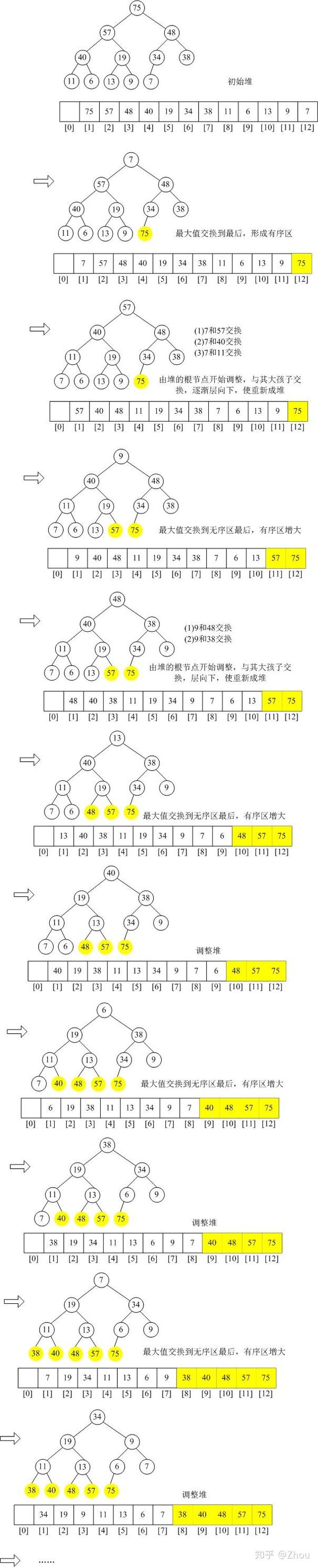
这个迭代持续直至最后一个元素即完成堆排序步骤。
代码展示
代码引自 数据结构示例——堆排序过程 。
void HeapSort(RecType R[],int n)
int i;
RecType temp;
//(1)循环建立初始堆
for (i=n/2; i>=1; i--)
sift(R,i,n);
//(2)进行n-1次循环,完成推排序
for (i=n; i>=2; i--)
temp=R[1]; //将第一个元素同当前区间内R[1]对换
R[1]=R[i];
R[i]=temp;
sift(R,1,i-1); //筛选R[1]结点,得到i-1个结点的堆
}伪代码
引用自 https://www. cc.gatech.edu/classes/c s3158_98_fall/heapsort.html
# 堆排序数组A
Heapsort(A) {
BuildHeap(A)
for i <- length(A) downto 2 {
exchange A[1] <-> A[i]
heapsize <- heapsize -1
Heapify(A, 1)
# 创建堆A
BuildHeap(A) {
heapsize <- length(A)
for i <- floor( length/2 ) downto 1
Heapify(A, i)
Heapify(A, i) {
le <- left(i)
ri <- right(i)
if (le<=heapsize) and (A[le]>A[i])
largest <- le
largest <- i
if (ri<=heapsize) and (A[ri]>A[largest])

