插值-上采样方法总结
一、理论原理
插值指的是利用已知数据去预测未知数据,图像插值则是给定一个像素点,根据它周围像素点的信息来对该像素点的值进行预测。当我们调整图片尺寸或者对图片变形的时候常会用到图片插值。比如说我们想把一个4x4的图片, 就会产生一些 新的像素点 ( 如下图红点所示),
如何给这些值赋值, 就是图像插值所要解决的问题
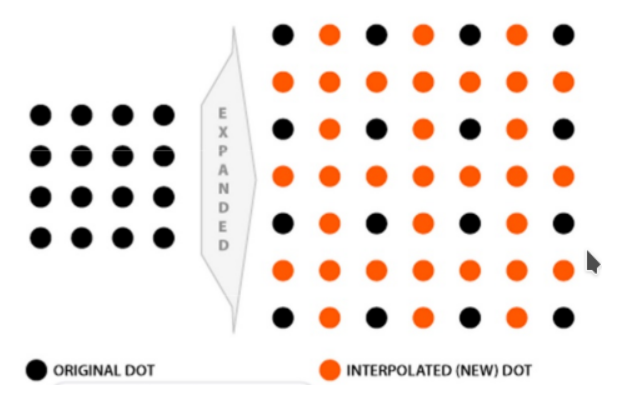
常见的插值算法可以分为两类: 自适应和非自适应 。
自适应的方法 可以根据插值的内容来改变(尖锐的边缘或者是平滑的纹理),自适应算法包括许可软件中的许多专有算法,例如:Qimage,PhotoZoom Pro和正版Fractals。
非自适应的方法 对所有的像素点都进行同样的处理。 非自适应算法包括:最近邻,双线性,双三次,样条,sinc,lanczos等。 由于其复杂度, 这些插值的时候使用从0 to 256 (or more) 邻近像素。 包含越多的邻近像素,他们越精确,但是花费的时间也越长。这些算法可以用来扭曲和缩放照片。
在做图像分割的时候,需要对图像进行像素级别的分类,因此在卷积提取到抽象特征后需要通过上采样将feature map还原到原图大小。
常见的上采样方法有
- 双线性插值、
- 转置卷积、
- 上采样(unsampling)和
- 上池化(unpooling)。
其中前两种方法较为常见,后两种用得较少。
下面对其进行简单介绍。
1、双线性插值
双线性插值 ,又称为 双线性内插 。
在 数学 上, 双线性插值 是对 线性插值 在二维 直角网格 上的扩展,用于对双变量函数(例如 x 和 y )进行 插值 。
其核心思想是在两个方向分别进行一次线性插值。
假设我们想得到未知函数 f 在点 P = (x, y) 的值,假设我们已知函数 f 在 Q11 = (x1, y1)、Q12 = (x1, y2), Q21 = (x2, y1) 以及 Q22 = (x2, y2) 四个点的值。
首先在 x 方向进行线性插值,得到:
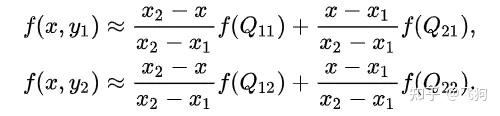
然后在 y 方向进行线性插值,得到 f(x, y):
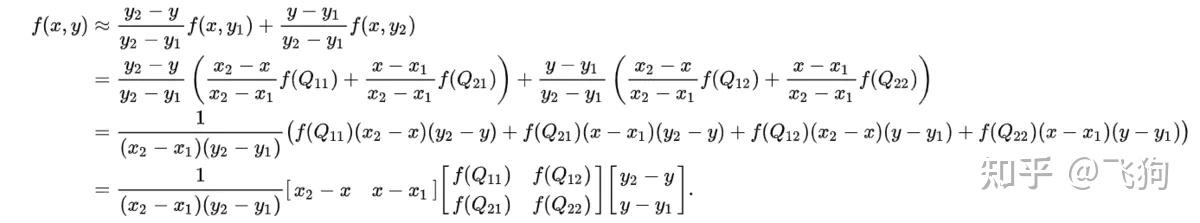
在FCN中上采样用的就是双线性插值。
2、转置卷积
在上面的双线性插值方法中不需要学习任何参数。而转置卷积就像卷积一样需要学习参数,关于转置卷积的具体计算可以参见 一文搞懂反卷积,转置卷积 。
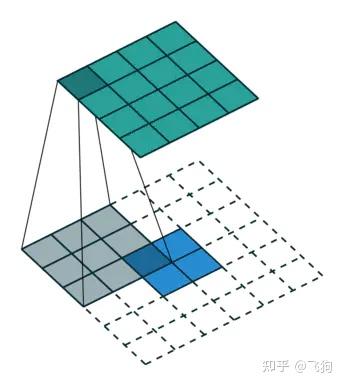
我们想要将输入矩阵中的一个值映射到输出矩阵的9个值,这将是一个一对多(one-to-many)的映射关系。这个就像是卷积操作的反操作,其核心观点就是用转置卷积。举个例子,我们对一个2 × 2 的矩阵进行上采样为4 × 4 的矩阵。这个操作将会维护一个1对应9的映射关系。
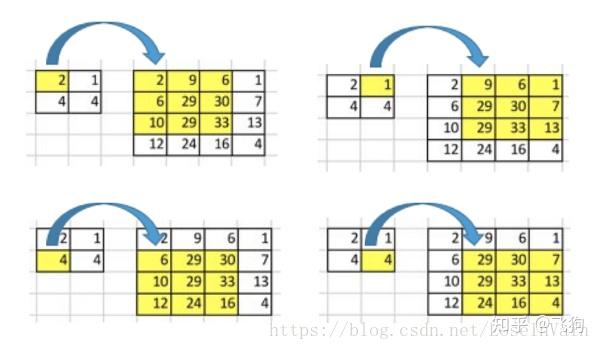
因此就结论而言,卷积操作是多对一,而转置卷积操作是一对多,如下图所示,每一个“对”而言,都需要维护一个权值。

但是我们将如何具体操作呢?为了接下来的讨论,我们需要定义一个卷积矩阵( convolution matrix )和相应的转置卷积矩阵( transposed convolution matrix )。
3、卷积矩阵
我们可以将一个卷积操作用一个矩阵表示。这个表示很简单,无非就是将卷积核重新排列到我们可以用普通的矩阵乘法进行矩阵卷积操作。如下图就是原始的卷积核:

我们对这个3 × 3 的卷积核进行重新排列,得到了下面这个4 × 16 的卷积矩阵:
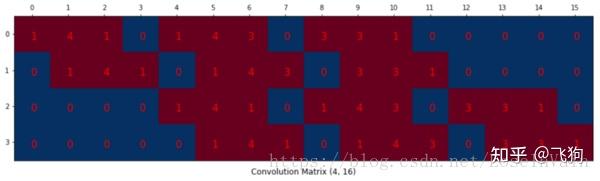
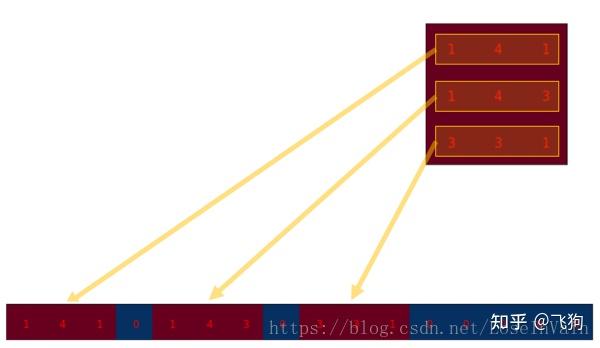
这个便是卷积矩阵了,这个矩阵的每一行都定义了一个卷积操作。下图将会更加直观地告诉你这个重排列是怎么进行的。每一个卷积矩阵的行都是通过重新排列卷积核的元素,并且添加0补充(zero padding)进行的。
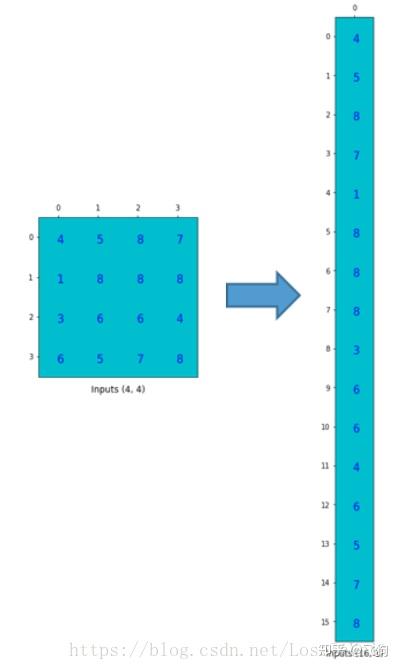
为了将卷积操作表示为卷积矩阵和输入矩阵的向量乘法,我们将输入矩阵4 × 4 4 \times 44×4摊平(flatten)为一个列向量,形状为16 × 1 16 \times 116×1,如下图所示。
我们可以将这个4 × 16 4 \times 164×16的卷积矩阵和1 × 16 1 \times 161×16的输入列向量进行矩阵乘法,这样我们就得到了输出列向量。
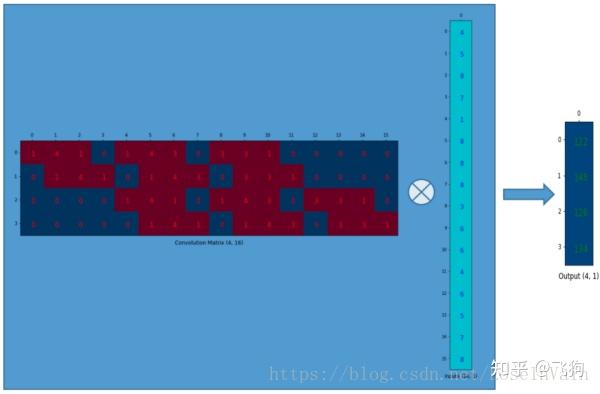
这个输出的4 × 1 4 \times 14×1的矩阵可以重新塑性为一个2 × 2 2 \times 22×2的矩阵,而这个矩阵正是和我们一开始通过传统的卷积操作得到的一模一样。

简单来说,这个卷积矩阵除了重新排列卷积核的权重之外就没有啥了,然后卷积操作可以通过表示为卷积矩阵和输入矩阵的列向量形式的矩阵乘积形式进行表达。
所以各位发现了吗,关键点就在于这个卷积矩阵,你可以从16(4 × 4 4 \times 44×4)到4(2 × 2 2 \times 22×2)因为这个卷积矩阵尺寸正是4 × 16 4 \times 164×16的,然后呢,如果你有一个16 × 4 16 \times 416×4的矩阵,你就可以从4(2 × 2 2 \times 22×2)到16(4 × 4 4 \times 44×4)了,这不就是一个上采样的操作吗?啊哈!让我们继续吧!
4、转置卷积矩阵
我们想要从4(2 × 2 2 \times 22×2)到16(4 × 4 4 \times 44×4),因此我们使用了一个16 × 4 16 \times 416×4的矩阵,但是还有一件事情需要注意,我们是想要维护一个1到9的映射关系。
假设我们转置这个卷积矩阵C ( 4 × 16 ) C \ \ (4 \times 16)C (4×16)变为C T ( 16 × 4 ) C^T \ \ (16 \times 4)C T (16×4)。我们可以对C T C_TC T 和列向量( 4 × 1 ) (4 \times 1)(4×1)进行矩阵乘法,从而生成一个16 × 1 16 \times 116×1的输出矩阵。这个转置矩阵正是将一个元素映射到了9个元素。
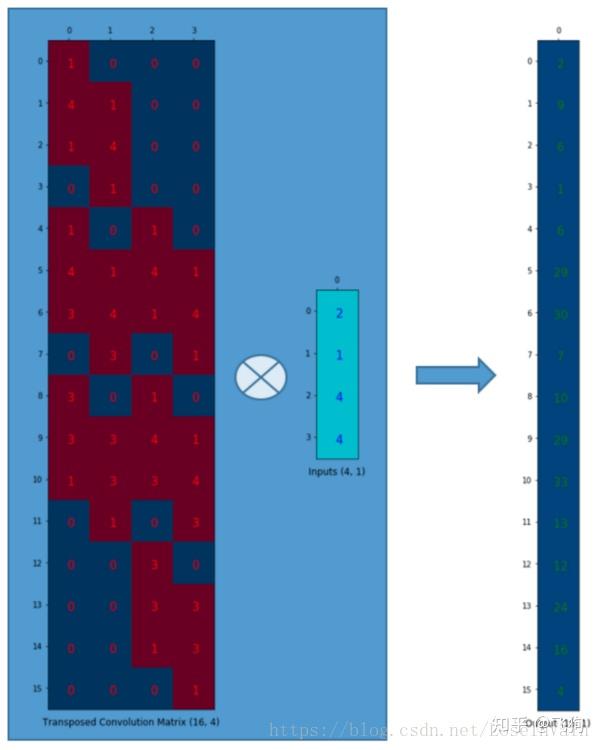
这个输出可以塑形为( 4 × 4 ) (4 \times 4)(4×4)的矩阵:
我们只是对小矩阵( 2 × 2 ) (2 \times 2)(2×2)进行上采样为一个更大尺寸的矩阵( 4 × 4 ) (4 \times 4)(4×4)。这个转置卷积矩阵维护了一个1个元素到9个元素的映射关系,因为这个关系正表现在了其转置卷积元素上。
需要注意的是:这里的转置卷积矩阵的参数,不一定从原始的卷积矩阵中简单转置得到的,转置这个操作只是提供了转置卷积矩阵的形状而已。
总结
转置卷积操作构建了和普通的卷积操作一样的连接关系,只不过这个是从反向方向开始连接的。我们可以用它进行上采样。另外,这个转置卷积矩阵的参数是可以学习的,因此我们不需要一些人为预先定义的方法。即使它被称为转置卷积,它并不是意味着我们将一些现存的卷积矩阵简单转置并且使用其转置后的值。
从本质来说,转置卷积不是一个卷积,但是我们可以将其看成卷积,并且当成卷积这样去用。我们通过在输入矩阵中的元素之间插入0进行补充,从而实现尺寸上采样,然后通过普通的卷积操作就可以产生和转置卷积相同的效果了。你在一些文章中将会发现他们都是这样解释转置卷积的,但是这个因为在卷积操作之前需要通过添加0进行上采样,因此是比较低效率的。
注意:转置卷积会导致生成图像中出现棋盘效应(checkerboard artifacts),这篇文章《Deconvolution and Checkerboard Artifacts》推荐了一种上采样的操作(也就是插值操作),这个操作接在一个卷积操作后面以减少这种现象。如果你的主要目的是生成尽可能少棋盘效应的图像,那么这篇文章就值得你去阅读。
补充内容
评论区有朋友提出了一个问题,我觉得可能有些朋友也会有类似的疑问因此在这里统一讨论下,问题为:
博主您好,我觉的转置卷积矩阵的参数随着训练过程不断被优化,但是它是在随机初始化的基础上进行优化,还是在原始卷积矩阵的基础上进行优化? – CSDN user BistuSim的博客_皮皮虾-_CSDN博客-android,深度学习,算法领域博主
这个问题其实可以通过观察深度学习框架的实现方式进行,我选用的是pytorch,我们打开torch.nn.ConvTranspose1d的源码,发现有:
class ConvTranspose1d(_ConvTransposeMixin, _ConvNd):
def __init__(self, in_channels, out_channels, kernel_size, stride=1,
padding=0, output_padding=0, groups=1, bias=True, dilation=1):
kernel_size = _single(kernel_size)
stride = _single(stride)
padding = _single(padding)
dilation = _single(dilation)
output_padding = _single(output_padding)
super(ConvTranspose1d, self).__init__(
in_channels, out_channels, kernel_size, stride, padding, dilation,
True, output_padding, groups, bias)
@weak_script_method
def forward(self, input, output_size=None):
# type: (Tensor, Optional[List[int]]) -> Tensor
output_padding = self._output_padding(input, output_size, self.stride, self.padding, self.kernel_size)
return F.conv_transpose1d(
input, self.weight, self.bias, self.stride, self.padding,
output_padding, self.groups, self.dilation)
不难发现其实我们的卷积核参数
weights
其实是在超类中定义的,我们转到
_ConvNd
,代码如:
class _ConvNd(Module):
__constants__ = ['stride', 'padding', 'dilation', 'groups', 'bias']
def __init__(self, in_channels, out_channels, kernel_size, stride,
padding, dilation, transposed, output_padding, groups, bias):
super(_ConvNd, self).__init__()
if in_channels % groups != 0:
raise ValueError('in_channels must be divisible by groups')
if out_channels % groups != 0:
raise ValueError('out_channels must be divisible by groups')
self.in_channels = in_channels
self.out_channels = out_channels
self.kernel_size = kernel_size
self.stride = stride
self.padding = padding
self.dilation = dilation
self.transposed = transposed
self.output_padding = output_padding
self.groups = groups
if transposed:
self.weight = Parameter(torch.Tensor(
in_channels, out_channels // groups, *kernel_size))
else:
self.weight = Parameter(torch.Tensor(
out_channels, in_channels // groups, *kernel_size))
if bias:
self.bias = Parameter(torch.Tensor(out_channels))
else:
self.register_parameter('bias', None)
self.reset_parameters()
我们可以清楚的发现,其实weights或者是bias的初始化就是一般地初始化一个符合一定尺寸要求的Tensor即可了,我们也可以发现其在forward过程中并没有所真的去根据输入进行权值的所谓“转置”之类的操作。因此我认为只要一般地进行 随机初始化 即可了。
而且,我们如果同时去观察torch.nn.Conv2d的类的话,其实也可以发现,其参数都是通过_ConvNd去进行初始化的,因此Conv2d和ConvTranspose2D的参数初始化除了尺寸的区别,其他应该类似。
5、unsampling和unpooling
unsampling和unpooling可以通过一个图来简单理解:

其中右侧为unsampling,可以看出unsampling就是将输入feature map中的某个值映射填充到输出上采样的feature map的某片对应区域中,而且是全部填充的一样的值。
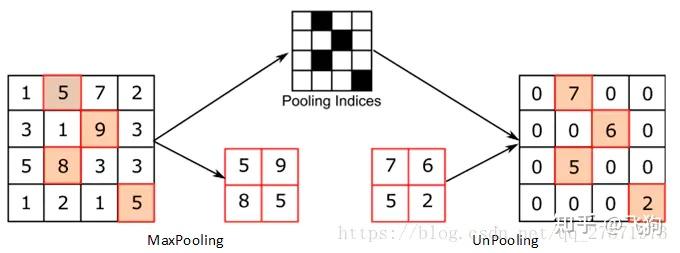
unpooling的操作与unsampling类似,区别是unpooling记录了原来pooling是取样的位置,在unpooling的时候将输入feature map中的值填充到原来记录的位置上,而其他位置则以0来进行填充。

二、 代数 多项式插值
对于大部分多项式插值函数,插值点的高度值可以视为所有(或某些)节点高度值的线性组合,而线性组合的系数一般是x坐标的多项式函数,称作基函数。
对于一个节点的基函数,它在x等于该节点的x时等于1,在x等于其他节点的x时等于0。这就保证曲线必定经过所有节点,所以属于内插方法。
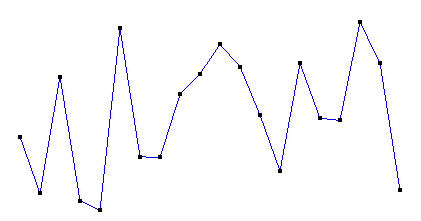
以一组随机数作为已知的高度值,使它们对应于间隔固定的x坐标,使用不同的插值函数获得各已知点(称为插值函数的节点)之外其它x坐标所对应的高度值,画出这些点所对应的曲线。再把所有高度值转换成灰度值,以颜色的变化比较各插值函数。
原点列如图:(假定横向为x,纵向为y。各点x坐标的间隔是固定的,但y坐标是随机的)

最简单的就是多项式插值:
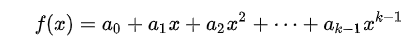
我们可以写出方程:
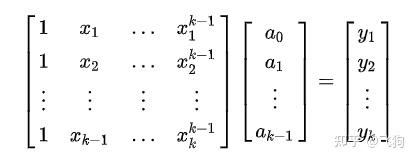
这里的已知是 x,y 要求的是 a, 求解线性方程组,既可得到答案。
多项式插值的问题肉眼可见,那就是基
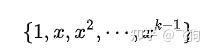
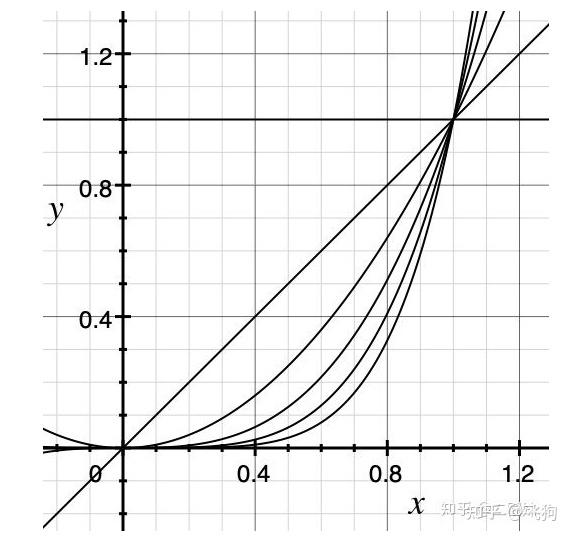
1、 线性插值
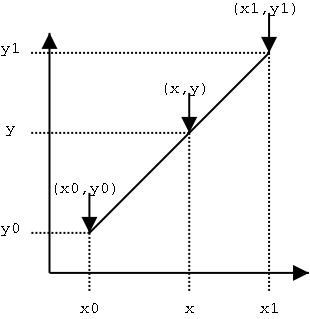
线性插值是用一系列首尾相连的线段依次连接相邻各点,每条线段内的点的高度作为插值获得的高度值。
以(xi,yi)表示某条线段的前一个端点,(x(i+1),y(i+1))表示该线段的后一个端点,则对于在[xi,x(i+1)]范围内的横坐标为x的点,其高度y为:
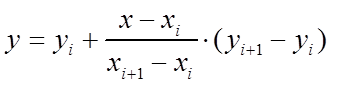
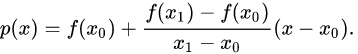
为便于与后面各函数比较,写成比较对称的形式:
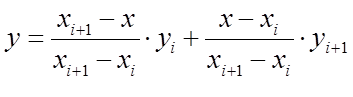
其中,yi和y(i+1)的两个参数称为基函数,二者之和为1,分别代表yi和y(i+1)对插值点高度的权值。
线性插值的特点是计算简便,但光滑性很差。
如果用线性插值 拟合 一条光滑曲线,对每一段线段,原曲线在该段内二阶导数绝对值的最大值越大,拟合的误差越大。
2、二次插值
如果按照线性插值的形式,以每3个相邻点做插值,就得到了二次插值:
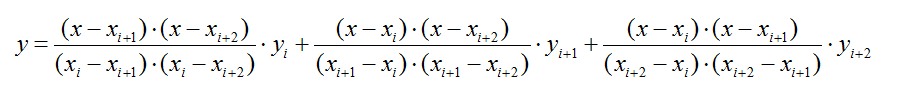
二次(分段)插值图像如下:
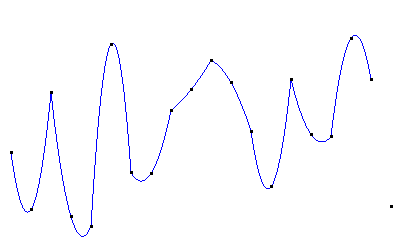
二次插值在每段二次曲线内是光滑的,但在每条曲线的连接处其光滑性可能甚至比线性插值还差。
二次插值只适合3个节点的情形,当节点数超过3个时,就需要分段插值了。
3、Cubic插值
如果想要保证各段曲线连接处光滑(一阶导数相同),并且不想使用除法运算,可以考虑Cubic插值函数:
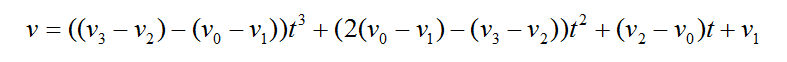
其中,v代表插值点,v0、v1、v2、v3代表4个连续的节点。
t取值为[0,1],将会产生一段连接v1和v2的曲线。
也就是说,如果有n个节点,Cubic插值函数将会产生(n-2)段曲线,位于首尾两端的节点不会纳入曲线
Cuibc插值图像如下:
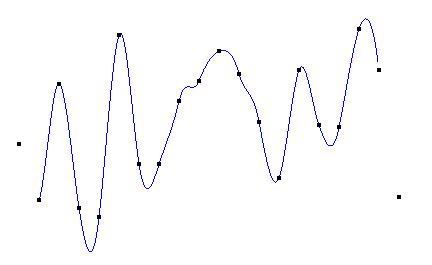
Cubic插值可以产生整体上光滑的曲线,但容易产生较剧烈的波动,使得曲线的最高点比最高的节点还高、曲线的最低点比最低的节点还低。
所以对颜色等取值有严格的上下界的数据进行插值时,会造成曲线的截取,破坏其光滑性。
比如颜色(RGB三个分量取值范围都是[0,255]),如果最高的节点是255,最低的节点是0,那么插值后负数会被截取成0,大于255的数会被截取成255。
4、拉格朗日插值法
解决插值函数的直接构造问题以及插值误差的估计问题,但是同时也使得插值函数值的计算变得复杂。
依照线性插值和二次插值的思路,可以增加基函数分子和分母的阶数,构造拉格朗日插值多项式
一般来说多项式插值就是求n-1个线性方程的解,拉格朗日插值即是基于此思想。拉格朗日创造性的避开的方程组求解的复杂性,引入“ 基函数 ”这一概念,使得快速手工求解成为可能。
DEF: 求作<=n 次多项式 pn(x),使满足条件pn(xi)= yi,i = 0,1,…,n.
这就是所谓拉格朗日( Lagrange)插值
先以一次(线性)为例,介绍基函数方法求解,再推广到任意次多项式:
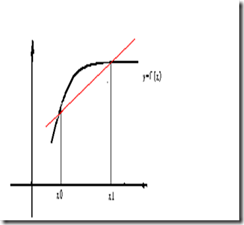
已知x0,x1;y0,y1,求P(x)= a0 + a1x,使得P(x)过这两点。则显然:
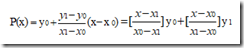
这里
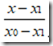
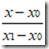
就是求解P(x)的两个基函数。
下面介绍基函数的一般形式 :
对于要求的插值函数P(x),可以证明,均可以化简为以下形式:
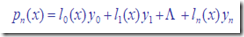
要使得:
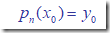
则要求:
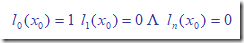
从而基函数表为:

从而,给出 基函数的一般形式 为:
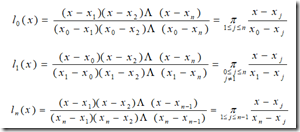
简而记之:
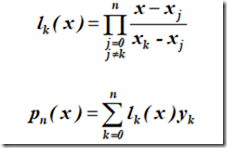
此即著名的 拉格朗日插值公式 。
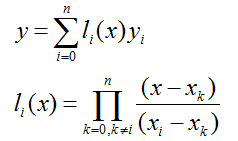
余项:
可以由罗尔定理(高数讲过的定理,忘记请自行google)等证明,拉格朗日插值的余项为:
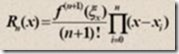
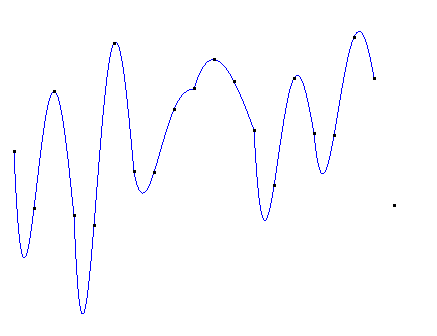
一个n次的拉格朗日插值函数可以绘制经过(n+1)个节点的曲线,但运算量非常大。
而且在次数比较高时,容易产生剧烈的震荡(龙格现象)。
所以要选择位置特殊的节点(比如切比雪夫多项式的零点)进行插值,或使用多个次数较低的拉格朗日函数分段插值。(关于拉格朗日多项式和龙格现象,详见维基百科链接)
Lagrange插值多项式的公式如下:
基函数:
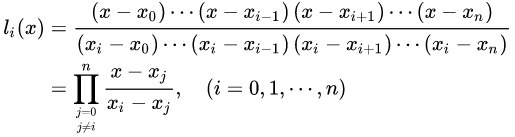
插值多项式:
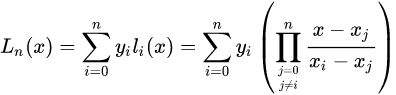
插值余项:
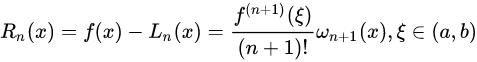
当 \max\limits_{a\leq{x}\leq{b}}|f^{n+1}(x)|=M_{n+1} 时,截断误差界是:
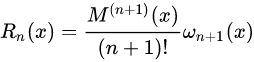
其中:
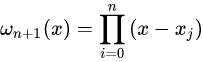
另一种多项式插值方法是把基选择为:
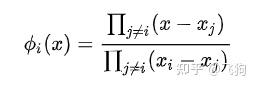
基满足:
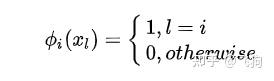
针对 拉格朗日 插值法一种简单的理解就是 多项式 * 多项式 依旧是多项式,而它的基也就是这样定的。用一个具体的例子,比如三个点会更加容易理解拉格朗日插值法。
这种多项式插值的问题在于:计算大,同时如果有两个点很靠近的话 x_i \approx x_j , 计算就会有较大的问题。当然上面提到的多项式插值的问题它也依旧存在。
多项式插值还有的问题包括:比如我们增加一个点,或者改变一个点,会对所有的系数a都产生影响,所以有了牛顿插值法。
使用4次拉格朗日多项式分段插值:
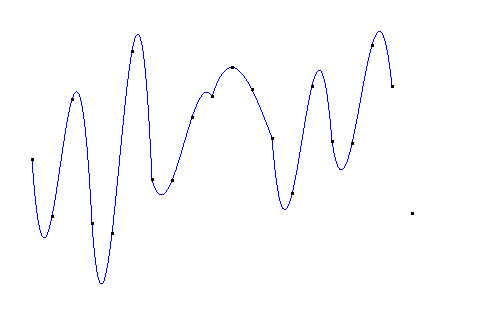
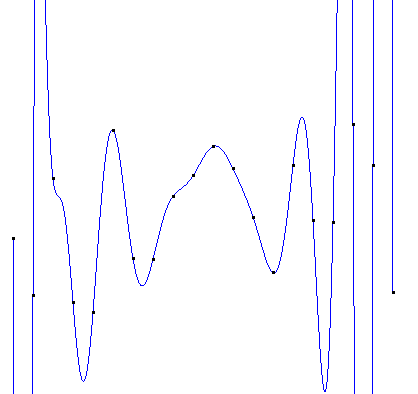
如果直接使用20次的拉格朗日插值,得到的图像如下:
三、牛顿插值法
从算法角度考虑,提出便于计算的插值方法,也就是牛顿插值公式。
拉格朗日插值每增加一个节点,整个函数要重新计算,计算量巨大。
而牛顿插值每增加一个点只需要在多项式的最后增加一项,而且各基函数的系数可以递归计算,减少了很多计算量。
1、均差(Divided differences)
是递归除法过程。在 数值分析 中,也称差商(Difference quotient),可用于计算牛顿多项式形式的多项式插值的系数。
定义
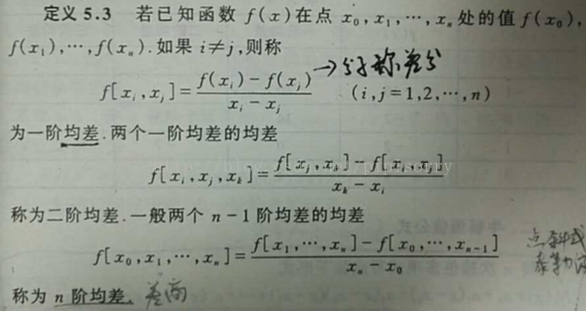
差商和差分的性质
一阶差商(均差):
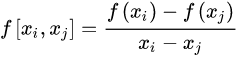
二阶差商(均差):一阶差商的差商
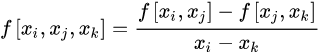
k 阶差商(均差):
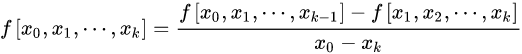
差商表(高阶差商是两个低一阶差商的差商)

2、牛顿多项式
将n次插值多项式写作如下形式:
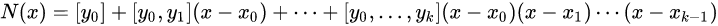
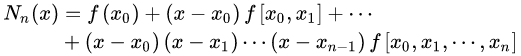

也就是牛顿插值公式中的各项系数就是均差表中计算出的各阶均差的第一个数据!
即牛顿插值公式为:
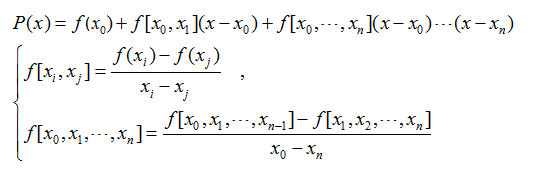
可能由于计算精度的原因,牛顿插值绘制的曲线与拉格朗日插值的曲线略有不同。
误差
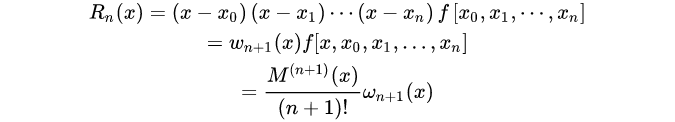
差商与导数的关系
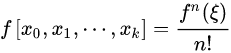
但次数较高时,牛顿插值也会产生剧烈的震荡。分段4次牛顿插值图像如下:
牛顿插值法的基我们写成:
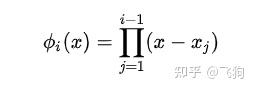
其中
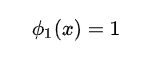
容易看出:
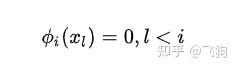
牛顿插值法的关键之处就是 我们只考虑跟它前面有关的点, 我们展开
可得线性方程组:
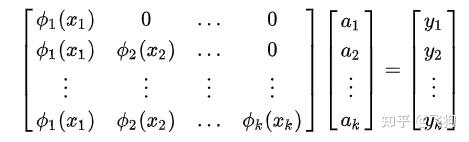
除了上面这些常见的插值基以外,我们还可以有,比如:
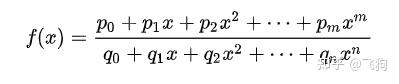
四、埃尔米特插值
以上各多项式插值方法的插值条件都是各节点的坐标,在以低阶函数分段插值时虽然可以保持曲线的稳定(比较平缓),但在各分段曲线的连接处无法保持光滑(一阶导数相等)。
埃尔米特插值方法不但规定了各节点的坐标值,还规定了曲线在每个节点的各阶导数,这样就可以既保持曲线的稳定,又保证在连接处足够光滑。
1、分段插值
分段插值可以说是 spline 的灵魂所在,感觉分段插值的好处是 local 性比较好,添加/减少/改变一个点 不会对全局影响那么高,个人感觉有限元的基础也是线性分段插值。
分段线性插值故名思议就是说把给定样本点的区间分成多个不同区间,记为[xi,xi+1],在每个区间上的一次线性方程为:
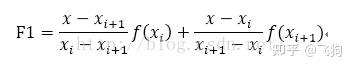
2、分段三次埃尔米特Hermite插值
以3次二重("m重"就是规定坐标和曲线在所有节点处1到m-1阶导数的值)埃尔米特插值为例:
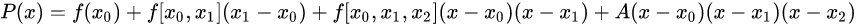
其中:
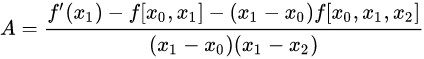
余项表达式:
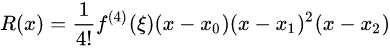
用Hermite进行插值时需要有确定的三个数据点以及中间点的一阶导数。
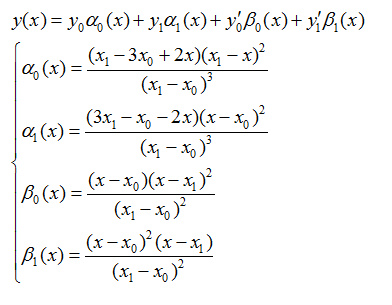
4个基函数满足分别只在y0,y1,y0的导数,y1的导数处等于1,而在其他3个条件下等于0。可以把埃尔米特插值看作对坐标和导数的插值的组合。
曲线在每个节点的导数可以根据相邻节点和它的相对位置确定,也可以完全随机生成。只要位置比较高和比较低的节点的导数绝对值不是很大,就可以使整条曲线落在最高与最低节点定义的带状区域内,这样就可以避免对插值的截取。
分段3次埃尔米特插值图像如下:
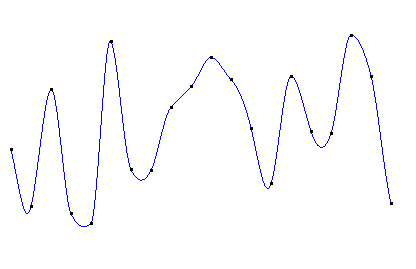
可见虽然n节点的埃尔米特插值是由(n-1)段曲线构成,但在每一个连接处都是光滑的。
五、 样条插值
1、B-样条
B-样条是Bezier样条的一般化,也可推广为NURBS样条。
先来介绍一下B-样条:
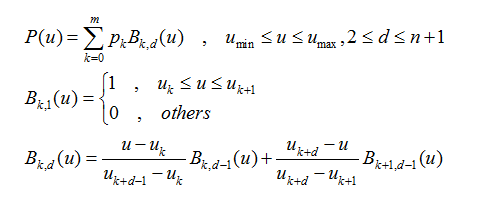
该式定义了一个n次的B-样条,它有(m+1)个控制点(样条曲线的“节点”称作控制点,因为这些点控制曲线的弯曲方向和程度,但曲线不一定经过这些点),也就有(m+1)个基函数。
一般绘制的是完整的曲线,u(min)取0,u(max)取1。
当u取值均匀时,该样条称作均匀B-样条。
当m=n时,B-样条退化为Bezier样条。
函数绘制的曲线始终落在其控制点的凸包(包含一个点集所有点的凸多边形,而且该凸多边形所有顶点都来自这个点集)中。
对于一个n次的B-样条,改变一个控制点的位置,只改变它所在的n段曲线(由n+1个控制点定义,且以该点起始)的形状,而不对其余的(m-n)段曲线产生影响。
2、Bezier样条
Bezier(贝塞尔)样条是法国工程师皮埃尔·贝塞尔(Pierre Bézier)在1962年为了设计汽车主体外形曲线而提出的。其一般式表达式为:
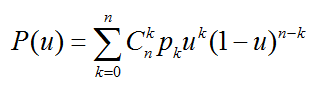
其中,u取值为[0,1],pk(k=0,...,n)为(n+1)个节点,n称为阶数。
Bezier样条还可以递归定义为:
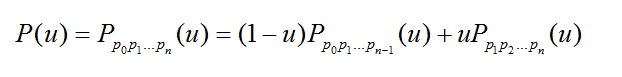
含义是n阶Bezier样条是两条(n-1)阶Bezier样条的插值。
当阶数降为1时,Bezier插值退化成线性插值。改变任意一个控制点的位置,整条曲线的形状都会发生变化。
- 三次样条插值
数学公式:
(1)求出点与点之间的公式: h(i)=x_{i+1}-x_{i}
(2) 计算二次微分值m
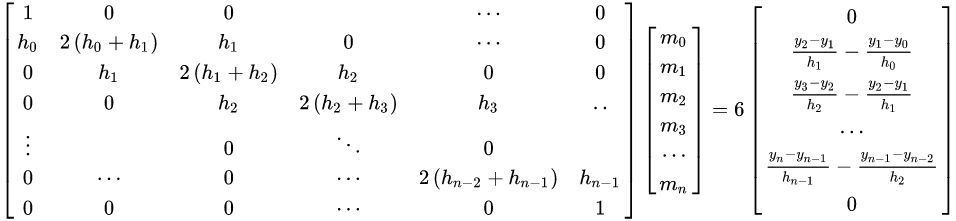
(3)计算系数
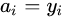
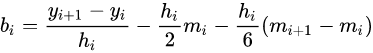
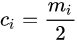
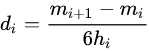
(4)计算样条函数
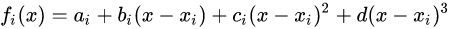
比较常用的Bezier样条是3次Bezier:
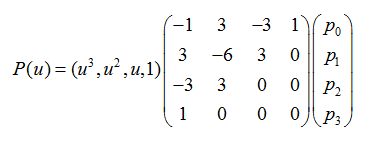
Beizer样条在首尾端的切线是前两个点和最后两个点的连线。
除了第一个点和最后一个点,其他控制点一般都不在曲线上。
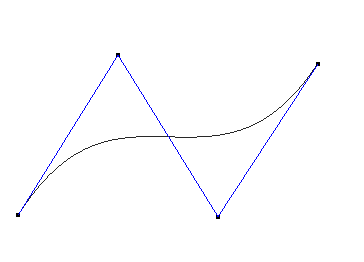
3阶(4控制点)的Bezier函数图像如下:(黑色曲线为Bezier曲线,蓝色折线为控制点的连线)
Bezier样条可以实现非常快速的运算。
为了方便说明,将3次Bezier样条表示成如下形式:
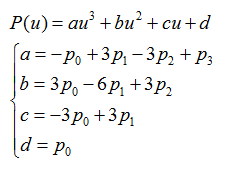
对于任意给定的u,可以通过合并的方式将原来的7次乘法、4次加法减少为3次乘法、3次加法:
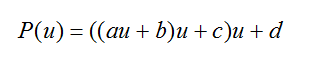
一般情况下,应用Bezier样条绘制曲线时,都是先给定一个很小的步长t(步长足够小才能保证Bezier曲线的精确),让t从0取到1,从头到尾绘制整条曲线。
在t不变的条件下,可以使用更快速的差分方法,利用前一个点计算出下一个点的值,将每步的计算量减小到只有3次加法:
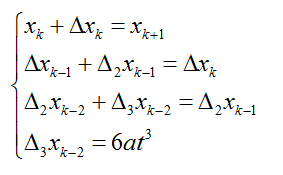
只需要在绘制曲线之前计算4个常数,就可以很快地计算出曲线上的所有点:
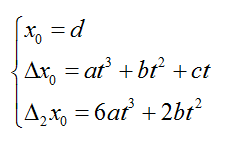
采用这种方式,Bezier样条的运算量只随阶数线性增长。
3、NURBS样条
NURBS(Non-Uniform Rational B-Splines 非均匀有理B-样条),是贝塞尔样条的推广。
“非均匀”的意思是控制点的间隔可以是不均匀的,
“有理”的意思是各控制点带有不同的权值。
和Bezier样条相比,它对曲线形状的控制更自由:
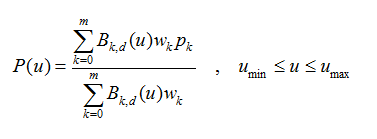
其基函数B(k,d)与B-样条的基函数相同,w(k)为各点的权因子。和B-样条一样,改变一个控制点的位置,只改变它所在的n段曲线的形状,而不对其余的(m-n)段曲线产生影响
六、opencv中插值函数
dst = cv2.resize(src,dsize,dst=None,fx=None,fy=None,interpolation=None)参数说明:
- src:输入图像
-
dsize:输出图像的大小。如果该参数为 0,表示缩放之后的大小需要通过公式计算,
dsize = Size(round(fx*src.cols),round(fy*src.rows))。其中fx与fy是图像 Width 方向和 Height 方向的缩放比例。 -
fx:Width 方向的缩放比例,如果是 0,按照
dsize * width/src.cols计算 -
fy:Height 方向的缩放比例,如果是 0,按照
dsize * height/src.rows计算 - interpolation:插值算法类型,或者叫做插值方式,默认为双线性插值
方法返回结果 dst 表示输出图像。
Interpolation
表示插值方式,有以下取值。
- INTER_NEAREST:最近邻插值
- INTER_LINEAR:线性插值(默认)
- INTER_AREA:区域插值
- INTER_CUBIC:4*4像素领域三次样条插值
- INTER_LANCZOS4:8*8像素领域Lanczos 插值
缩小时推荐使用 cv2.INTER_AREA
扩展放大时推荐使用 cv2.INTER CUBIC 和 cv2.INTER LINEAR,前者比后者运行速度慢。
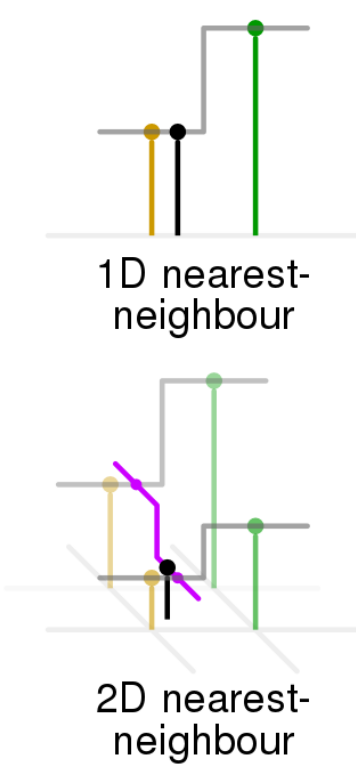
INTER_NEAREST:最近邻插值
这是最简单的一种插值方法,不需要计算,在待求象素的四邻象素中,将距离待求象素最近的邻象素灰度赋给待求象素。
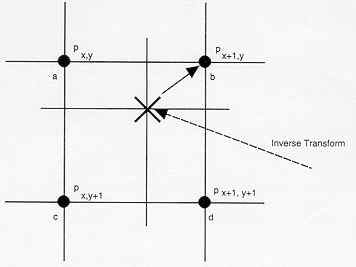
设i+u, j+v(i, j为正整数, u, v为大于零小于1的小数,下同)为待求象素坐标,则待求象素灰度的值 f(i+u, j+v) 如下图所示:
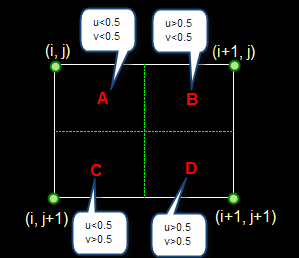
如果(i+u, j+v)落在A区,即u<0.5, v<0.5,则将左上角象素的灰度值赋给待求象素,
同理,落在B区则赋予右上角的象素灰度值,落在C区则赋予左下角象素的灰度值,落在D区则赋予右下角象素的灰度值。
最邻近元法计算量较小,但可能会造成插值生成的图像灰度上的不连续,在灰度变化的地方可能出现明显的锯齿状
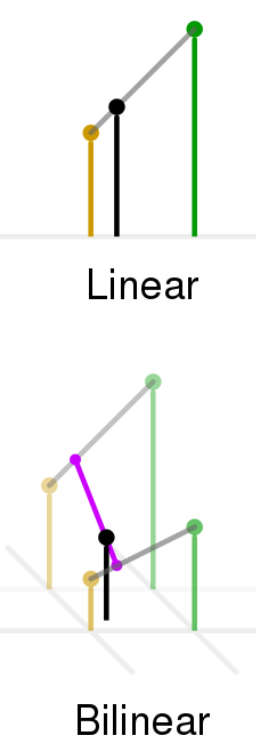
NTER_LINEAR(默认):(双)线性插值
双线性内插法是利用待求象素四个邻象素的灰度在两个方向上作线性内插,
如下图所示:
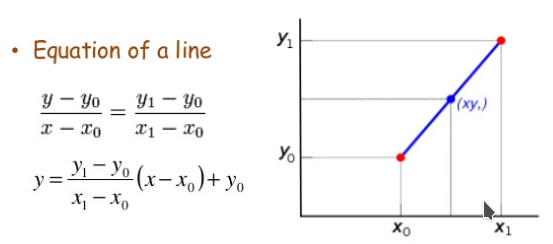
以距离为权重的一种插值方式。已知数据 (x0, y0) 与 (x1, y1),要计算 [x0, x1] 区间内某一位置 x 在直线上的y值:
把上边的式子整理得:
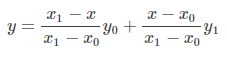
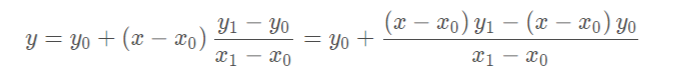
这个式子的意思就是用x和x0,x1的距离作为一个权重,用于y0和y1的加权。双线性插值本质上就是在两个方向上做线性插值。
其实,即使x不在x0到x1之间,这个公式也是成立的。在这种情况下,这种方法叫作线性外插。
线性插值的误差:线性插值其实就是拉格朗日插值有2个结点时的情况。插值余项为:
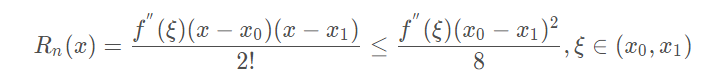
从插值余项可以看出,随着二阶导数的增大,线性插值的误差增大。即函数的曲率越大,线性插值近似的误差也越大。
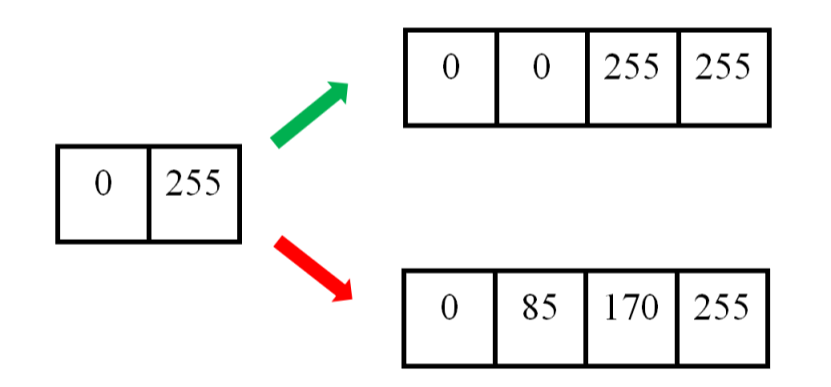
举个例子。下图中,左边为原图像,拉伸后,理想的输出图像的像素分布应该为绿色箭头指向的,但是按照线性插值,会得到红色箭头指向的结果。
双线性插值
在数学上,双线性插值是有两个变量的插值函数的线性插值扩展,其核心思想是在两个方向分别进行一次线性插值。
双线性插值形式:
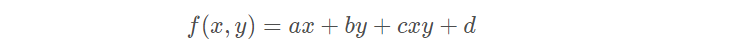
双线性插值是线性插值在二维时的推广,在两个方向上共做了三次线性插值。定义了一个双曲抛物面与四个已知点拟合。
具体操作为在X方向上进行两次线性插值计算,然后在Y方向上进行一次插值计算。见下图:
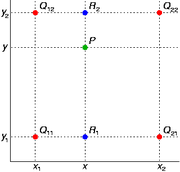
我们想得到未知函数 f 在点 P = (x, y) 的值,假设我们已知函数 f 在 Q11 = (x1, y1)、Q12 = (x1, y2), Q21 = (x2, y1) 以及 Q22 = (x2, y2) 四个点的值。最常见的情况,f就是一个像素点的像素值。思路是我们可以将求解过程分解为两次插值过程,首先在x轴方向上进行插值,根据点Q11,Q21得到
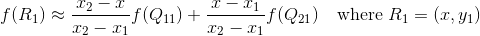
根据点Q12,Q22得到
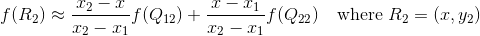
然后在y轴方向上进行插值, 根据点R1 和R2得到
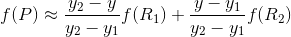
整理得
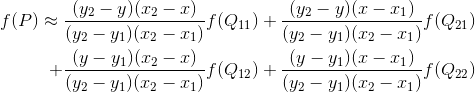
对于 (i, j+v),f(i, j) 到 f(i, j+1) 的灰度变化为线性关系,则有:
f(i, j+v) = [f(i, j+1) - f(i, j)] * v + f(i, j)
同理对于 (i+1, j+v) 则有:
f(i+1, j+v) = [f(i+1, j+1) - f(i+1, j)] * v + f(i+1, j)
从f(i, j+v) 到 f(i+1, j+v) 的灰度变化也为线性关系,由此可推导出待求象素灰度的计算式如下:
f(i+u, j+v) = (1-u) * (1-v) * f(i, j) + (1-u) * v * f(i, j+1) + u * (1-v) * f(i+1, j) + u * v * f(i+1, j+1)
双线性内插法的计算比最邻近点法复杂,计算量较大,但没有灰度不连续的缺点,结果基本令人满意。
它具有低通滤波性质,使高频分量受损,图像轮廓可能会有一点模糊。
INTER_AREA:区域插值-像素关系重采样
cv2.INTER_AREA
在缩小和放大图像时,是完全不一样的。
- 缩小图像
指的是输出图像的宽和高都不大于输入图像的宽和高。
缩小比例是不是整数倍(当然是在指scale_x和scale_y,因为输出图像小)。
- 缩小比例是整数倍
在这种情况下,有个boolean variable
is_area_fast
会被设定为
true
。之后的实际计算就会调用并行优化的方法。
然后我们还要再分情况:
1.调用的interpolation是INTER_LINEAR_EXACT 时,如果宽和高的缩小比例都是2,并且图像的通道数量不是2,那么实际会调用INTER_AREA。
2.调用的 interpolation 是 INTER_LINEAR 时,如果宽和高的缩小比例都是2,那么实际会调用 INTER_AREA。
3.INTER_AREA是 box filter (average filter)
首先我们把一个RGB图像看成个立方体,在深度方向上我们排列三个通道。取图像其中的一行,它看上去就像图
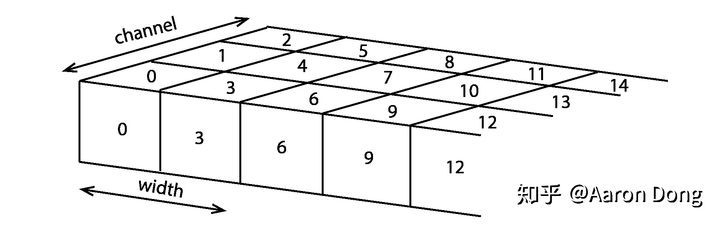
一个RGB图像的一行,每一个格子代表一个像素,其上的数字代表index,或者在一行上的index的偏移量(offset)。
每个格子代表一个像素,其上的数字代表像素的index,或者也可以看成在某一行上的index的偏移量(offset)。OpenCV里用了一个指向array的指针
xofs
(可能代表x of source或者x offset),被指向的array里存的就是一行的indices,这些indices记录了一个区域的开始的位置,这个区域就是后面用来计算输出图像像素的。比如说,我们想把图像的宽和高都缩到原来的三分之一,那么
iscale_x = 3
,
iscale_y = 3
。然后这个区域就是个3乘3的block,结果就是
xofs
记录下的indices为0、1、2、9、10、11,等等。对比图1,这几个数就是在
x
方向上,一个3乘3的block从哪里开始。
然后OpenCV算了一个变量
area = iscale_x * iscale_y
。按我们前面的例子,
area = 9
。
另外一个指向array的指针
ofs
指向的array包含了
area
这么多个元素。这些数字是每个通道上,构成一个block的那些像素的index的offset。假如我们的输入图像宽是9个像素的话,仍然缩小为三分之一,那
ofs
指向的值就是0、3、6、27、30、33、54、57、60。
当我们计算好了这些offsets之后,就开始计算输出图像的像素了。其实这一步所做的事情非常好理解,我们现在已经划好了区域,输出图像的像素就是这个block包括进来的输入图像的像素的平均值。就像图2所示。
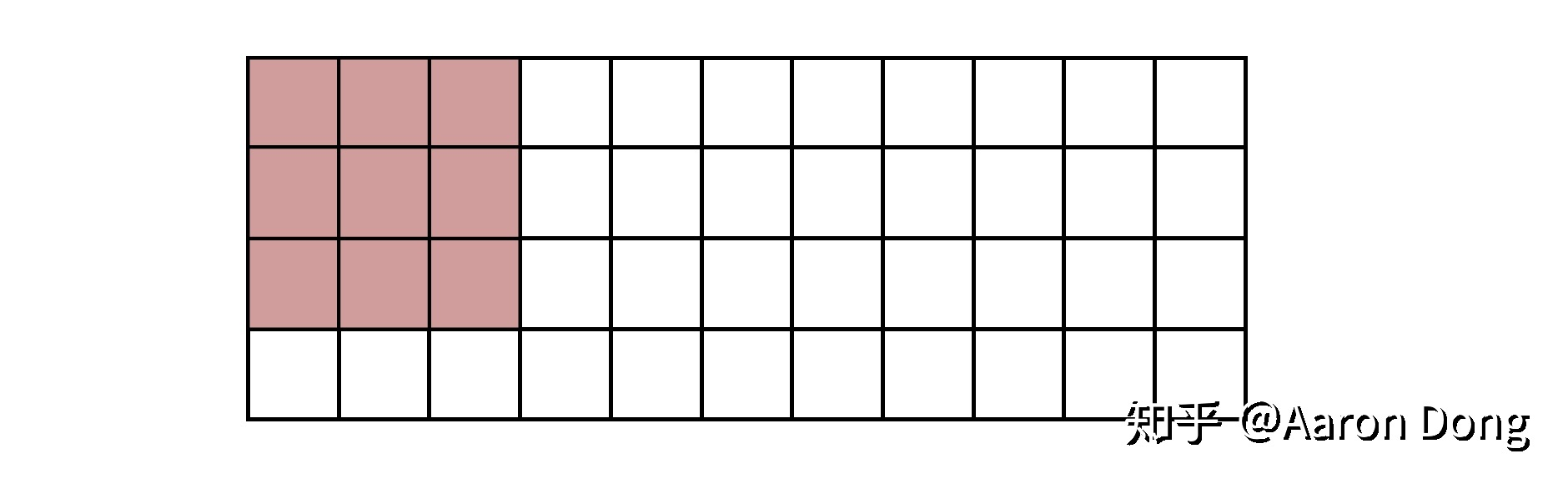
输入图像的一部分。假设缩小宽和高为原来的三分之一,红色部分即为一个block。这个区域内的像素值的平均值,为输出图像的像素值。
对输出图像的宽方向上的每个位置
dx
,我们取出
xofs
的一个值,根据这个值,加上
ofs
中记录的block的构成的偏移量,我们可以得到block是输入图像的哪些像素,之后取平均值,重复每个通道。之后移动到
x
方向的下一个位置,按我们的缩为三分之一的例子,就是位置9(注意,这不是图像的卷积,所以不是移动一个格子)。
- 缩小比例不是整数倍
当缩小比例不是整数倍的时候的情况。每一种颜色代表block在不断移动到下一个位置的情形。例如下图1维图像情况:

当缩小比例不是整数倍的时候的情况。每一种颜色代表block在不断移动到下一个位置的情形。
block有多大就取多大,下一个位置就紧挨着上一个位置的边界取。
- 放大图像
当用
INTER_AREA
来放大图像时,实际调用的是
INTER_LINEAR
,只是线性插值的系数和正常算法不一样。
1维的图像,在高方向上做法完全一样。对线性的方法来说,一个像素值是由它左右两侧的像素值的线性函数得到的。距离一个像素越近,则系数(权重)越大。在继续讨论
INTER_AREA
之前,我想先说说在OpenCV里
INTER_LINEAR
的系数是怎么算出来的。
在OpenCV里,对每一个输出图像在
x
方向的位置
dx
,右边像素的系数(线性插值用左右两边像素的值)的算法代码:
fx = (float)((dx+0.5)*scale_x - 0.5); // (1)
sx = cvFloor(fx); // (2)
fx -= sx; // (3)
注意
scale_x
是输入图像的宽除以输出图像的宽的比值(放大图像时小于1)。这里其实还牵扯到functional programming经常提到的一个特点,就是变量的值是不变的,而命令式则经常改变变量的值。这里(1)和(3)都在算
fx
,但其实
fx
的意思前后已经发生了变化。
(1)中的
fx
是输入图像在
x
方向的坐标,
(3)中的是线性插值右边像素的系数(左边的像素的系数是
1-fx
)。
(1)这个式子是怎么来的?我们看图
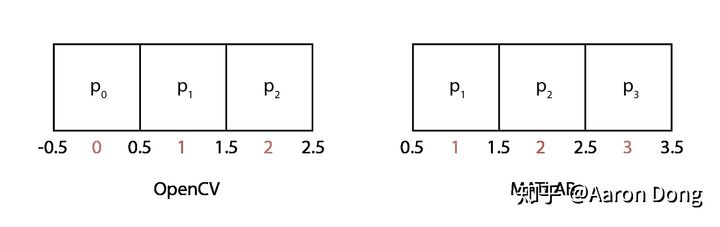
1维图像的坐标系(index)。左边为OpenCV(C++),右边为MATLAB。我们让像素值位于格子中间,并给格子的边界赋予坐标。
展示的是1维图像的坐标系。我们把像素值放在格子中间,同时让格子的边界也有自己的坐标。在C++里,index从0开始,在MATLAB里,index从1开始。
(1)所做的是把输出图像的坐标(每一个
dx
)映射成输入图像的坐标。因为这是个线性函数,所以我们需要两个等式来确定这个函数。第一个等式来自于我们要求输入图像和输出图像的左侧边界的坐标一致。那也就是说输出图像坐标空间的-0.5对应输入图像坐标空间的-0.5。于是
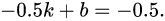
第二个等式来自于我们要求输出图像坐标空间中
inv_scale_x
这么长的距离,在输入图像坐标空间中应该等于1.于是
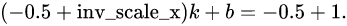
联立求解,即可得这个线性函数,进而得到(1)。因为MATLAB中index从1开始,所以MATLAB里是这样计算的:
u = x/scale + 0.5 * (1 - 1/scale);
这里
scale
相当于
inv_scale_x
。这段代码在
images.internal.resize.contributions
中。
所以, [0,1] 放大2倍其实会变成 [0,0.25,0.75,1] 。图5显示了放大2倍时,100个(其实是101个)输出图像的位置的左侧像素的系数。
然而
INTER_AREA
的系数不是这样算的。我们还需要讨论一下放大倍数是不是整数。
- 放大比例是整数倍
系数为(1,0)的线性插值(复制左侧/上方像素)。
对输出图像的每一个像素位置
dx
,系数是这样算的:
sx = cvFloor(dx*scale_x);
fx = (float)((dx+1) - (sx+1)*inv_scale_x); // (4)
fx = fx <= 0 ? 0.f : fx - cvFloor(fx);以及
cbuf[0] = 1.f - fx;
cbuf[1] = fx;
cbuf
存的是左侧和右侧像素的系数。因为
inv_scale_x
是整数,(4)相当于
int inv_scale_x_integer = saturate_cast<int>(inv_scale_x);
fx = dx % inv_scale_x_integer + 1 - inv_scale_x_integer;也就是
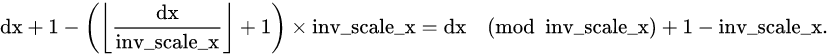
因为
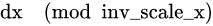
最大为
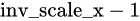
fx
最大就是0.再加上这句
fx = fx <= 0 ? 0.f : fx - cvFloor(fx);
fx
就只会等于0.这样
cbuf[0] = 1
,
cbuf[1]=0
,也就是说,线性插值的系数始终是左边的像素为1,右边的为0,于是结果就是始终在复制左边的像素值。
- 放大比例不是整数倍
线性插值,大部分系数为(1,0)。
如果放大比例不是整数倍,那么系数就不只是1和0了,但是大部分会是。整个过程仍然类似于整数倍的情形,只是这时取余的模成了实数。虽然除以实数是没有什么余数的,但我们可以类比整数的情况把整个实数看作一个整体。图6显示了当放大比例是5.6时,101个输出图像位置的左侧像素的系数。
INTER_CUBIC:4×4邻域双三次样条插值
给定n+1个点,a=x_0<x_1<...<x_n=b,以及他们的函数值f(x_i),i=0,1,2,...n上,确定一个三次多项式:
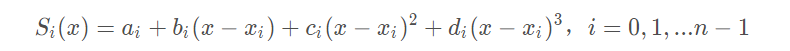
每个三次多项式中有四个未知参数,有n个区间,n个多项式,共4n个未知参数。
我们知道“n个未知数需要n个已知条件确定唯一解”,所以要确定这4n个未知参数,共需要4n个已知条件。
每个三次多项式满足如下条件:

以上共4n−2个条件,还差2个条件,由如下三种边界条件确定:
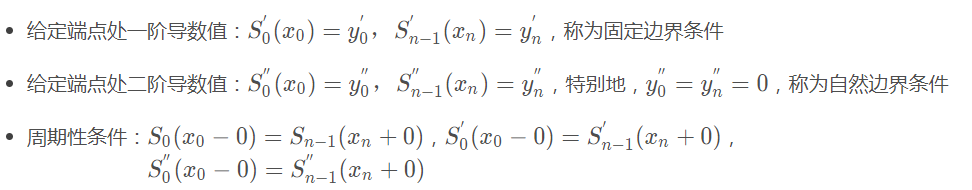
4n个条件有了,就可以确定每个区间上的三次多项式。
对于每个区间内的点,就可以用Si(x)得到插值结果。
该方法利用三次多项式S(x)求逼近理论上最佳插值函数sin(x)/x, 其数学表达式为:
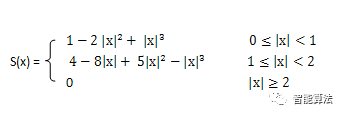
待求像素(x, y)的灰度值由其周围16个灰度值加权内插得到,如下图:
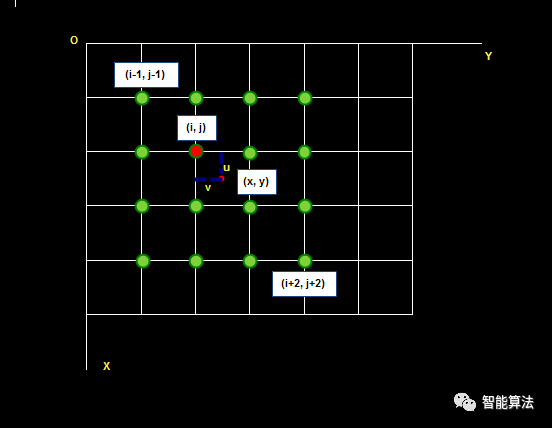
假设源图像A大小为m*n,缩放后的目标图像B的大小为M*N。那么根据上边提到的方法我们可以得到B(X,Y)在A上的对应坐标为
A(x,y)=A(X*(m/M),Y*(n/N))
在双线性插值法中,我们选取A(x,y)的最近四个点。而在双三次插值法中,我们选取的是最近的16个像素点作为计算目标图像B(X,Y)处像素值的参数。
如图所示:
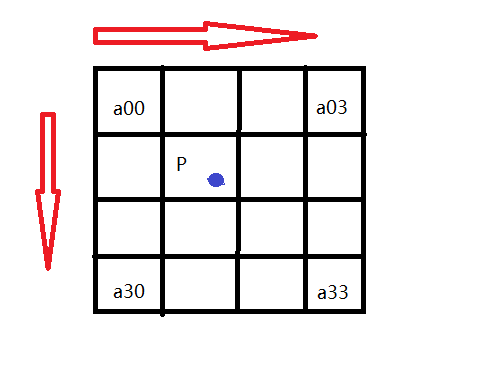
如图所示P点就是目标图像B在(X,Y)处对应于源图像A中的位置, 假设P的坐标为(i+u,j+v),其中i,j分别表示整数部分,u,v分别表示小数部分。
找到如图所示距离p最近的16个像素的位置,在这里用a(m,n)(m,n=0,1,2,3)来表示。
双立方插值的目的就是通过找到一种关系,或者说系数,可以把这16个像素对于P处像素值得影响因子找出来,从而根据这个影响因子来获得目标图像对应点的像素值,达到图像缩放的目的。
我在这次的学习中学习的是基于BiCubic基函数的双三次插值法,
BiCubic基函数形式如下:
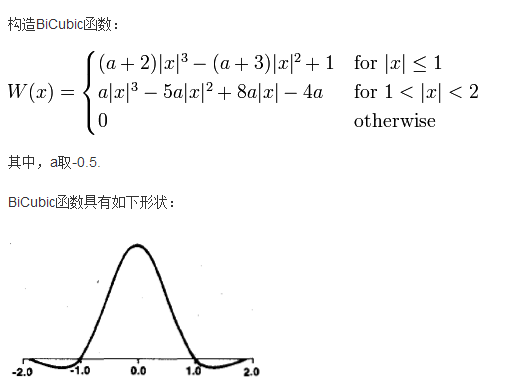
我们要做的就是找到BiCubic函数中的参数x,从而获得上面所说的16个像素所对应的系数。
在学习双线性插值法的时候,我们是把图像的行和列分开来理解的,那么在这里,我们也用这种方法描述如何求出a(m,n)对应的系数k_m_n。
假设行系数为k_m,列系数为k_n。
我们以a00位置为例:
首先,我们要求出当前像素与P点的位置,比如a00距离P(i+u,j+v)的距离为(1+u,1+v)。
那么a00的横坐标权重k_m_0=W(1+u),纵坐标权重k_n_0=W(1+v).
同理我们可以得到所有行和列对应的系数:
k_m_0=W(1+u), k_m_1=W(u), k_m_2=W(1-u), k_m_3=W(2-u);
k_n_0=W(1+v), k_n_1=W(v), k_n_2=W(1-v), k_n_3=W(2-v);
这样我们就分别得到了行和列方向上的系数。
由横纵坐标权重的乘积可以得到每个像素a(m,n)对应的权值了。
比如a00对B(X,Y)的贡献值为:(a00像素值)* k_m_0* k_n_0
最后通过求和公式可以得到目标图片B(X,Y)对应的像素值:
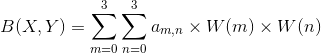
其中W(m)表示amn横坐标上的权重,W(n)表示amn纵坐标上的权重。三次曲线插值方法相较于前面的最近邻和线性插值而言计算量较大,但插值后的图像效果最好。
待求像素的灰度计算式如下:
f(x, y) = f(i+u, j+v) = ABC
其中:
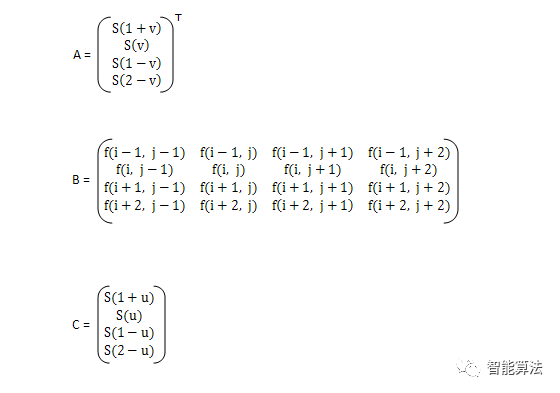
三次曲线插值方法计算量较大,但插值后的图像效果最好。
三次样条插值具有良好的收敛性,稳定性和光滑性,优点明显,是非常重要的插值工具。
INTER_LANCZOS4:Lanczos 插值-傅立叶变换有关的三角函数的方法8*8像素邻域
七、pytorch中 插值函数
nn.Upsample
CLASS torch.nn.Upsample(size=None, scale_factor=None, mode='nearest', align_corners=None)
上采样一个给定的多通道的 1D (temporal,如向量数据), 2D (spatial,如jpg、png等图像数据) or 3D (volumetric,如点云数据)数据
假设输入数据的格式为minibatch x channels x [optional depth] x [optional height] x width。因此对于一个空间spatial输入,我们期待着4D张量的输入,即minibatch x channels x height x width。而对于体积volumetric输入,我们则期待着5D张量的输入,即minibatch x channels x depth x height x width
对于上采样有效的算法分别有对 3D, 4D和 5D 张量输入起作用的 最近邻、线性,、双线性, 双三次(bicubic)和三线性(trilinear)插值算法
你可以给定scale_factor来指定输出为输入的scale_factor倍或直接使用参数size指定目标输出的大小(但是不能同时制定两个)
参数:
- size ( int or Tuple[ int ] or Tuple[ int , int ] or Tuple[ int , int , int ], optional ) – 根据不同的输入类型制定的输出大小
- scale_factor ( float or Tuple[ float ] or Tuple[ float , float ] or Tuple[ float , float , float ], optional ) – 指定输出为输入的多少倍数。如果输入为tuple,其也要制定为tuple类型
-
mode
(
str
,
optional
) – 可使用的上采样算法,有
'nearest','linear','bilinear','bicubic'and'trilinear'.默认使用'nearest' -
align_corners
(
bool
,
optional
) – 如果为True,输入的角像素将与输出张量对齐,因此将保存下来这些像素的值。仅当使用的算法为
'linear','bilinear'or'trilinear'时可以使用。默认设置为False
输入输出形状:
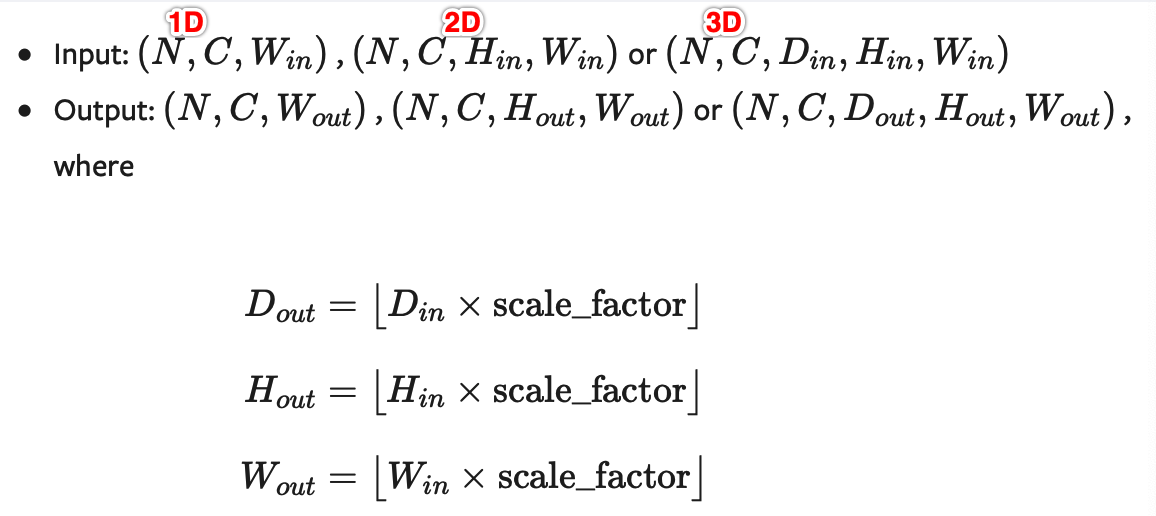
用例:

注意:
当align_corners = True时,线性插值模式(线性、双线性、双三线性和三线性)不按比例对齐输出和输入像素,因此输出值可以依赖于输入的大小。这是0.3.1版本之前这些模式的默认行为。从那时起,默认行为是align_corners = False,如下图:
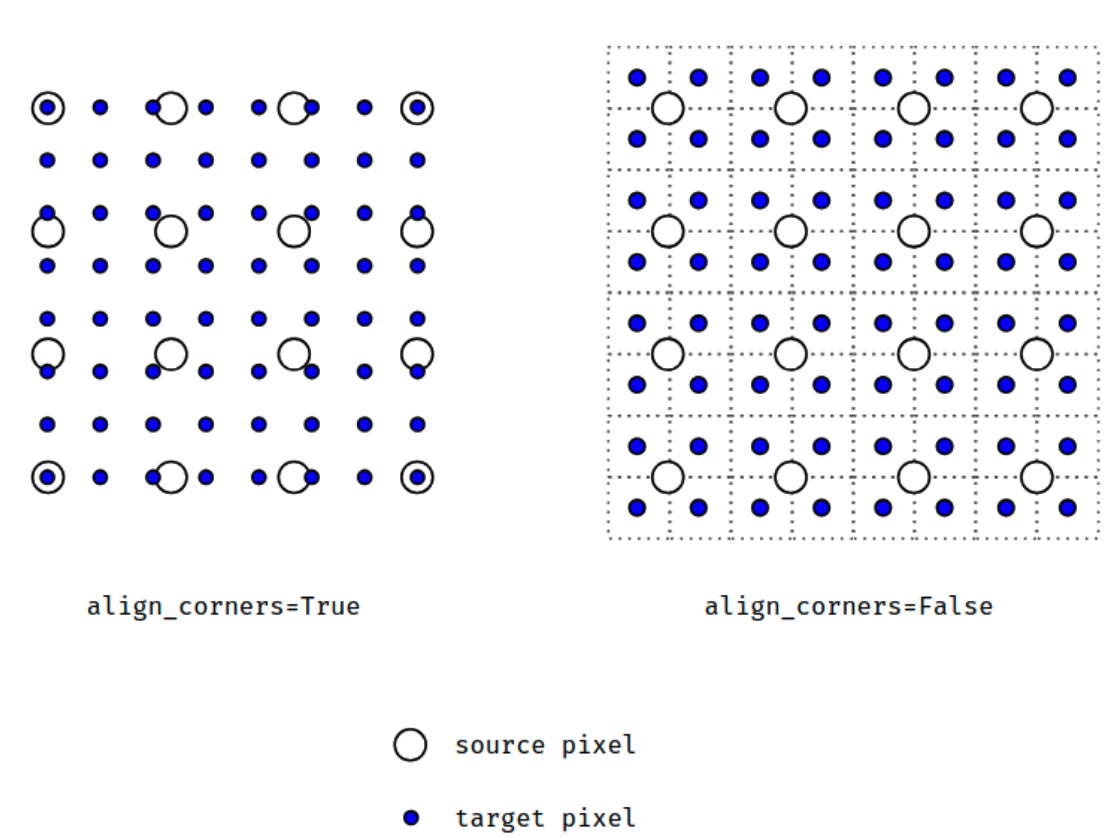
上面的图是source pixel为4*4上采样为target pixel为8*8的两种情况,这就是对齐和不对齐的差别,会对齐左上角元素,即设置为align_corners = True时输入的左上角元素是一定等于输出的左上角元素。
但是有时align_corners = False时左上角元素也会相等,官网上给的例子就不太能说明两者的不同(也没有试出不同的例子,大家理解这个概念就行了)
如果您想下采样/常规调整大小,您应该使用interpolate()方法,这里的上采样方法已经不推荐使用了。
nn.UpsamplingNearest2d
如果你使用的数据都是JPG等图像数据,那么你就能够直接使用2D数据的方法:
CLASS torch.nn.UpsamplingNearest2d(size=None, scale_factor=None)专门用于2D数据的线性插值算法,参数等跟上面的差不多,省略
形状:
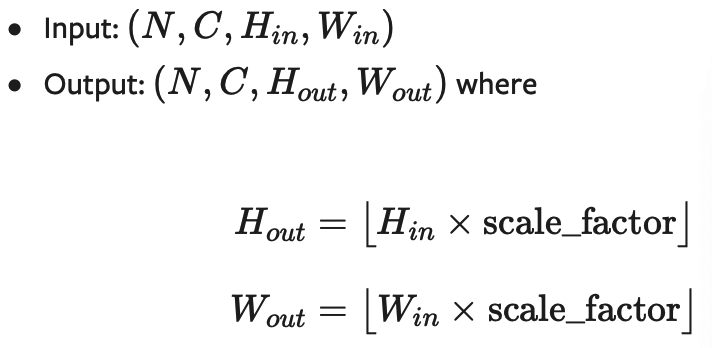
nn.UpsamplingBilinear2d
CLASS torch.nn.UpsamplingBilinear2d(size=None, scale_factor=None)专门用于2D数据的双线性插值算法,参数等跟上面的差不多,省略
形状:
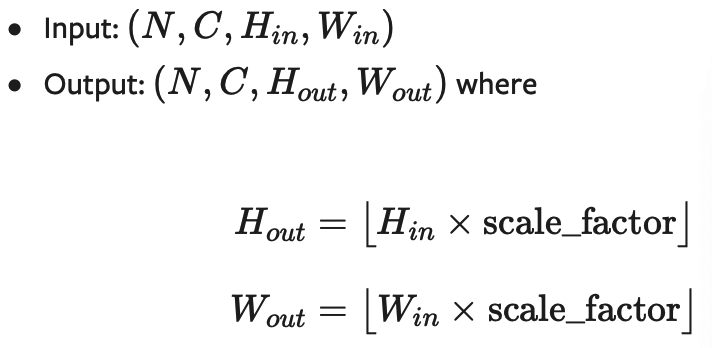
nn.functional.interpolate
torch.nn.functional.interpolate(
input,
