python运筹优化（一）：Cplex for python使用简介

wuxiaojun

粤港澳大湾区数字经济研究院 NLP算法工程师

运筹学(OR)和优化模型包括线性规划(LP)、混合整数线性规划(MILP)和二次规划(QP)。一般我们使用LP/MILP包来单独建模一个实际的优化问题，例如GAMS、AMPL、OPL或其他，然后使用优化求解器(例如CPLEX、gu、Mosek、Xpress等)来解决它，并将最优结果提供给经理和决策者。

在OR和数据科学社区中，许多人推荐使用Python这种优秀且流行的编程语言。它简单、灵活、功能强大，并且拥有大量用于机器学习、优化和统计建模的库。在本文中，我将重点介绍如何使用Python编写或建模(LPs/MILPs)。

许多优化解决程序(商业的和开源的)都有用于建模LPs、MILPs和QPs的Python接口。这里我选择了CPLEX和Gurobi，因为它们都是领先的商业解决方案，还有PuLP，它是Python中一个强大的开源建模包。我将为每个包提供一个并行教程，我希望它能帮助您轻松地将模型从一个转换到另一个。在这里，我们使用gurobipy (Gurobi的Python API)、docplex(用于Python的IBM Decision Optimization CPLEX建模包)和pulp(用Python编写的LP/MILP建模器)。出于本文的目的，我假设您熟悉Python，即，您知道如何安装和使用Python包，以及使用Python数据结构，如列表、元组和字典。我还将假设您知道线性规划、混合整数规划和约束优化的基本知识。

快速回顾一下，优化模型是一个具有目标(或多目标编程中的一组目标)、一组约束和一组决策变量的问题。下面是一个简单的优化模型:

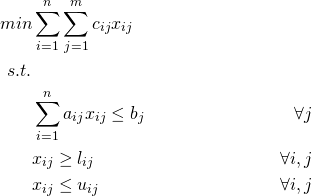
在上述优化例子中，n、m、a、c、l、u、b为输入参数，假设为给定。为了编写Python代码，我们将这些参数设置如下:

有10*5个决策变量Xij，10行5列

import random
n = 10
m = 5
set_I = range(1, n+1)
set_J = range(1, m+1)
c = {(i,j): random.normalvariate(0,1) for i in set_I for j in set_J}
a = {(i,j): random.normalvariate(0,5) for i in set_I for j in set_J}
l = {(i,j): random.randint(0,10) for i in set_I for j in set_J}
u = {(i,j): random.randint(10,20) for i in set_I for j in set_J}
b = {j: random.randint(0,30) for j in set_J}

现在是时候在Python中实现我们的OR模型了。当我们想要编写一个优化模型时，我们为该模型放置一个占位符(就像一个空白画布)，然后将其元素(决策变量和约束)添加到其中。这里是:

1、导入运筹优化库

import docplex.mp.model as cpx
opt_model = cpx.Model(name="MIP Model")

2、定义决策变量

接下来我们主要以cplex为例讲解：

在这一步之后，我们有一个名为opt_model的模型对象。接下来，我们需要添加决策变量。在Python字典(或panda系列)中存储决策变量是标准的，其中字典键是决策变量，值是决策变量对象。一个决策变量由三个主要属性定义:它的类型(连续、二进制或整数)、它的下界(默认为0)和上界(默认为无穷大)。对于上面的例子，我们可以将决策变量定义为:

# if x is Continuous
x_vars  = 
{(i,j): opt_model.continuous_var(lb=l[i,j], ub= u[i,j],
                                 name="x_{0}_{1}".format(i,j)) 
for i in set_I for j in set_J}
# if x is Binary
x_vars  = 
{(i,j): opt_model.binary_var(name="x_{0}_{1}".format(i,j)) 
for i in set_I for j in set_J}
# if x is Integer
x_vars  = 
{(i,j): opt_model.integer_var(lb=l[i,j], ub= u[i,j],
                              name="x_{0}_{1}".format(i,j)) 
for i in set_I for j in set_J}

3、约束条件

在设置决策变量并将它们添加到我们的模型之后，就到了设置约束的时候了。任何约束都有三个部分:左手边(通常是决策变量的线性组合)、右手边(通常是数值)和意义(小于或等于、等于、大于或等于)。要设置任何约束，我们需要设置每个部分:

# <= constraints，小于等于
constraints = {j : 
opt_model.add_constraint(
ct=opt_model.sum(a[i,j] * x_vars[i,j] for i in set_I) <= b[j],
ctname="constraint_{0}".format(j))
    for j in set_J}
# >= constraints
constraints = {j : 
opt_model.add_constraint(
ct=opt_model.sum(a[i,j] * x_vars[i,j] for i in set_I) >= b[j],
ctname="constraint_{0}".format(j))
    for j in set_J}
# == constraints
constraints = {j : 
opt_model.add_constraint(
ct=opt_model.sum(a[i,j] * x_vars[i,j] for i in set_I) == b[j],
ctname="constraint_{0}".format(j))
    for j in set_J}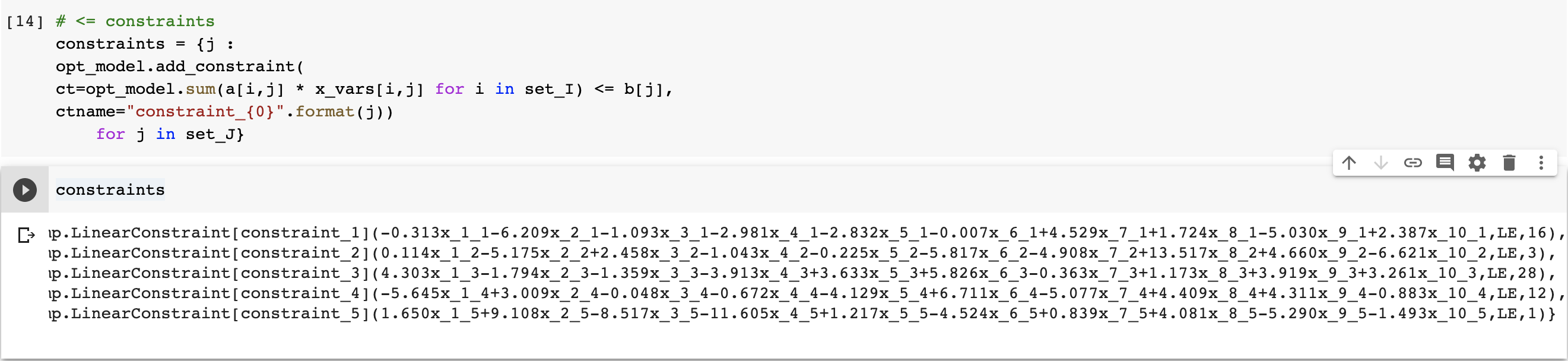

4、目标函数

下一步是定义一个目标，它是一个线性表达式。我们可以这样定义目标:

objective = opt_model.sum(x_vars[i,j] * c[i,j] 
                          for i in set_I 
                          for j in set_J)
# for maximization             
opt_model.maximize(objective)
# for minimization
opt_model.minimize(objective)

5、求解模型

# solving with local cplex
opt_model.solve()
# solving with cplex cloud
opt_model.solve(url="your_cplex_cloud_url", key="your_api_key")

6、获得结果

现在我们完成了。我们只需要得到结果并进行后期处理。panda包是一个很好的数据处理库。如果问题得到最优解，我们可以得到和处理结果如下:

import pandas as pd
opt_df = pd.DataFrame.from_dict(x_vars, orient="index", 
                                columns = ["variable_object"])opt_df.index = 
pd.MultiIndex.from_tuples(opt_df.index, 
                               names=["column_i", "column_j"])opt_df.reset_index(inplace=True)