如何通俗易懂地介绍 Gaussian Process？

这篇回答节选自我的专栏 《机器学习中的数学：概率图与随机过程》 ，我们来仔细介绍和分析一下高斯过程。

欢迎关注我的知乎账号 @石溪 ，将持续发布机器学习数学基础及算法应用等方面的精彩内容。

高斯过程，从字面上分解，我们就可以看出他包含两部分：

第一：高斯，指的是高斯分布

第二：过程，指的是随机过程

我们回过头来重新梳理一下整个高斯分布的脉络：

首先当随机变量是1维的时候，我们称之为一维高斯分布，概率密度函数 p(x)=N(\mu,\sigma^2) ，当随机变量的维度上升到有限的 p 维的时候，就称之为高维高斯分布， p(x)=N(\mu,\Sigma_{p\times p}) 。而高斯过程则更进一步，他是一个定义在连续域上的无限多个高斯随机变量所组成的随机过程，换句话说，高斯过程是一个无限维的高斯分布。

我们用符号来更严谨的进行描述：

对于一个连续域 T （假设他是一个时间轴），如果我们在连续域上任选 n 个时刻： t_1,t_2,t_3,...,t_n\in T ，使得获得的一个 n 维向量 \{\xi_1,\xi_2,\xi_3,...,\xi_n\} 都满足其是一个 n 维高斯分布，那么这个 \{\xi_t\} 就是一个高斯过程。

下面我们来实际举一个例子，让大家更能直观的建立高斯过程的印象，下面的图中，横轴 T 是一个关于时间的连续域，表示人的一生，而纵轴表示的是体能值，对于同一个人种的男性而言，在任意不同的时间点体能值都服从正态分布，但是不同时间点分布的均值和方差不同。

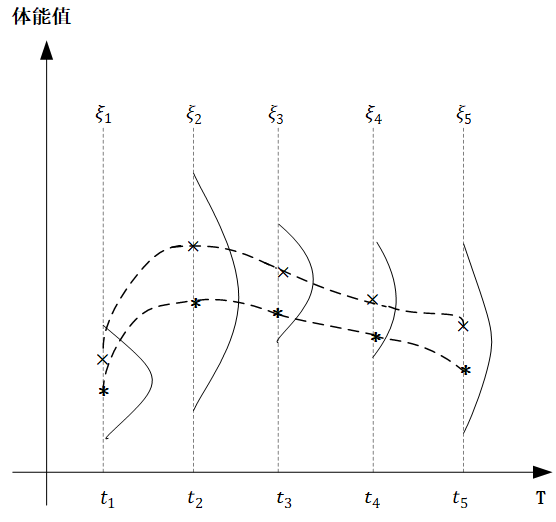
图中，我们取出了 t_1,t_2,t_3,t_4,t_5 五个时间点，分别代表同一个男性群体童年、少年、青年、中年、老年的具体时刻， \xi_1,\xi_2,\xi_3,\xi_4,\xi_5 分别对应五个时刻的体能值，他们都服从高斯分布，只不过从图中可以看出，均值和方差都不同，那么概率起来：

对于任意 t\in 连续时间轴T ， \xi_t\sim N(\mu_t,\sigma^2_t) ，也就是对于一个确定的高斯过程而言，对于任意时刻 t ，他的 \mu_t 和 \sigma^t 都已经确定了。而像上图中，我们对同一人种男性体能值在关键节点进行采样，然后平滑连接，也就是图中的两条虚线，就形成了这个高斯过程中的两个样本。

import numpy as np
def gaussian_kernel(x1, x2, l=1.0, sigma_f=1.0):
    m, n = x1.shape[0], x2.shape[0]
    dist_matrix = np.zeros((m, n), dtype=float)
    for i in range(m):
        for j in range(n):
            dist_matrix[i][j] = np.sum((x1[i] - x2[j]) ** 2)
    return sigma_f ** 2 * np.exp(- 0.5 / l ** 2 * dist_matrix)
train_X = np.array([1, 3, 7, 9]).reshape(-1, 1)#转换为4*1矩阵形式
print(gaussian_kernel(train_X, train_X))

[[1.00000000e+00 1.35335283e-01 1.52299797e-08 1.26641655e-14]
 [1.35335283e-01 1.00000000e+00 3.35462628e-04 1.52299797e-08]
 [1.52299797e-08 3.35462628e-04 1.00000000e+00 1.35335283e-01]
 [1.26641655e-14 1.52299797e-08 1.35335283e-01 1.00000000e+00]]

关注 @石溪 知乎账号，分享更多机器学习数学基础精彩内容。

最后我们来看高斯过程回归

这个过程我们其实可以看作是一个先验+观测值，然后推出后验的过程，怎么讲？

我们先通过 \mu(t) 和 k(s,t) 定义一个高斯过程，但是因为此时并没有任何的观测值，所以这是一个先验：

那么，如果我们获得了一组观测值之后，如何来修正这个高斯过程的均值函数和核函数，使之得到他的后验过程呢？

我们先回顾一下高维高斯分布的条件概率，我们知道，高斯分布有一个很好的特性，那就是高斯分布的联合概率、边缘概率、条件概率仍然是满足高斯分布的，假设：

n 维的随机变量满足高斯分布： x\sim N(\mu,\Sigma_{n\times n})

那么如果我们把这个 n 维的随机变量分成两部分： p 维的 x_a 和 q 维的 x_b ，满足 n=q+p ，那么按照均值向量 \mu 和协方差矩阵 \Sigma 的分块规则，就可以写成：

x=\begin{bmatrix}x_a\\x_b\end{bmatrix}_{p+q}\quad\mu=\begin{bmatrix}\mu_a\\\mu_b\end{bmatrix}_{p+q}\quad \Sigma=\begin{bmatrix}\Sigma_{aa}&\Sigma_{ab}\\\Sigma_{ba}&\Sigma_{bb}\end{bmatrix}

那么依据高斯分布的性质，我们知道下列条件分布依然是一个高维的高斯分布：

x_b|x_a\sim N(\mu_{b|a},\Sigma_{b|a})

\mu_{b|a}=\Sigma_{ba}\Sigma^{-1}_{aa}(x_a-\mu_a)+\mu_b

\Sigma_{b|a}=\Sigma_{bb}-\Sigma_{ba}\Sigma^{-1}_{aa}\Sigma_{ab}

也就是说，设置了高斯过程的先验参数，一旦我们拿到一些观测值，那么就可以对高斯过程的均值函数和核函数进行修正，得到一个修正后的后验高斯过程，而更新后验参数的信息就来自于观测值。

那么将高斯过程对比高维高斯分布，我们把均值向量替换成均值函数，把协方差矩阵替换成核函数，就能够得到高斯过程基于观测值的后验过程的参数表达式：

我们的一组观测值，他们的时刻对应一个向量 X ，那么对应的值时另一个同纬度的向量的 Y ，假设有4组观测值，那就是 \{(X[1],Y[1]),((X[2],Y[2])),((X[3],Y[3])),((X[4],Y[4]))\}

那么余下的所有非观测点，在连续域上我们定义为 X^* ，值定义为 f(X^*)

首先，联合分布显然是满足无限维高斯分布的：

\begin{bmatrix}Y\\f(X^*)\end{bmatrix}\sim N(\begin{bmatrix}\mu(X)\\\mu(X^*)\end{bmatrix}，\begin{bmatrix}k(X,X)& k(X,X^*)\\k(X^*,X)&k(X^*,X^*)\end{bmatrix})

从这个联合分布所派生出来的条件概率 f(X^*)|Y 同样也服从高斯分布，当然这里指的是无限维高斯分布，其实对比一下，把 Y 看作是 x_a ，把 f(X^*) 看作是 x_b ，直接类比条件分布的参数表达式： f(X^*)|Y\sim N(\mu^*,k^*)

这里面的 \mu^* 和 k^* 就是条件分布下的后验高斯过程的均值函数和核函数的形式。

类比我们就可以写成表达式：

\mu^*=k(X^*,X)k(X,X)^{-1}(Y-\mu(X))+\mu(X^*)

k^*=k(X^*,X^*)-k(X^*,X)k(X,X)^{-1}k(X,X^*)

好了，公式堆的够多了，下面我们来实际的进行代码演示，在我们的例子中，高斯过程先验，我们设置均值函数为 \mu(X)=0 ，径向基函数 k(X,X^*)=\sigma^2exp(-\frac{||X-X^*||^2}{2l^2}) 中的超参数为 l=0.5 ， \sigma=0.2 。

然后我们 X=[1,3,7,9] 的位置上设置一组观测值， Y 为$X$取正弦的基础上加上一点高斯噪声。

y=0.4sin(x)+N(0,0.05)

我们在四个观测点的基础上，来求高斯过程的后验。在下面的具体程序实现中，由于绘图是离散化处理的，因此连续域上的均值函数以及核函数，我们使用一个 n 很大的 n 维均值向量以及 n\times n 协方差矩阵进行表示的：

代码片段：

import matplotlib.pyplot as plt
import numpy as np
#高斯核函数
def gaussian_kernel(x1, x2, l=0.5, sigma_f=0.2):
    m, n = x1.shape[0], x2.shape[0]
    dist_matrix = np.zeros((m, n), dtype=float)
    for i in range(m):
        for j in range(n):
            dist_matrix[i][j] = np.sum((x1[i] - x2[j]) ** 2)
    return sigma_f ** 2 * np.exp(- 0.5 / l ** 2 * dist_matrix)
#生成观测值，取sin函数没有别的用意，单纯就是为了计算出Y
def getY(X):
    X = np.asarray(X)
    Y = np.sin(X)*0.4 + np.random.normal(0, 0.05, size=X.shape)
    return Y.tolist()
#根据观察点X，修正生成高斯过程新的均值和协方差
def update(X, X_star):
    X = np.asarray(X)
    X_star = np.asarray(X_star)
    K_YY = gaussian_kernel(X, X)  # K(X,X)
    K_ff = gaussian_kernel(X_star, X_star)  # K(X*, X*)
    K_Yf = gaussian_kernel(X, X_star)  # K(X, X*)
    K_fY = K_Yf.T # K(X*, X) 协方差矩阵是对称的，因此分块互为转置
    K_YY_inv = np.linalg.inv(K_YY + 1e-8 * np.eye(len(X)))  # (N, N)
    mu_star = K_fY.dot(K_YY_inv).dot(Y)
    cov_star = K_ff - K_fY.dot(K_YY_inv).dot(K_Yf)
    return mu_star, cov_star
f, ax = plt.subplots(2, 1, sharex=True,sharey=True)
#绘制高斯过程的先验
X_pre = np.arange(0, 10, 0.1)
mu_pre = np.array([0]*len(X_pre))
Y_pre = mu_pre
cov_pre = gaussian_kernel(X_pre, X_pre)
uncertainty = 1.96 * np.sqrt(np.diag(cov_pre))#取95%置信区间
ax[0].fill_between(X_pre, Y_pre + uncertainty,Y_pre - uncertainty, alpha=0.1)
ax[0].plot(X_pre, Y_pre, label="expection")
ax[0].legend()
#绘制基于观测值的高斯过程后验
X = np.array([1, 3, 7, 9]).reshape(-1, 1)#4*1矩阵
Y = getY(X)
X_star = np.arange(0, 10, 0.1).reshape(-1, 1)
mu_star, cov_star = update(X, X_star)
Y_star = mu_star.ravel()