在平时编程过程中会遇到很多非线性无法利用cplex和gurobi等求解器求解的问题，这时可以通过线性化处理的方式来转换模型，进而采用常规线性化工具进行求解，本文重点对三种非线性的问题进行转化，分别是乘积线性化、绝对值线性化和平方线性化，在每类线性化的理论公式下列出相应的yalmip程序代码，以供大家参考。

1 乘积线性化

2 绝对值线性化

3 平方线性化

1 乘积线性化

虽然两个01变量相乘，但是在yalmip求解时也会被认为是非线性，这就需要按照下式进行简化：

程序代码如下：

x1=binvar(1);

x2=binvar(1);

y=binvar(1);

con=[y<=x1,y<=x2,y>=x1+x2-1];

上述即实现了模型的程序语言化，由于仅做了模型的转化，作为程序应用示例，上面代码并不能单独运行，还需要增加相应目标函数等其他代码才能完全运行，具体可运行程序可参见文后链接）。

不难发现，1.1是1.2情况的一种特例，单拿出来分析的原因在于实际处理比较多，按照1.1来实现1.2的代码并不难，在此不再赘述。

除了上述最简单的程序代码处理之外，考虑实际电力系统情形，在程序编写过程中，会遇到发电机组启停与功率的乘积项，两个参数均为变量，这就需要对其进行线性化处理，具体程序代码如下（程序仅为示例，介绍用法，并不能单独运行，有些变量赋值不全，详情可参见最终全部程序代码）：

%onoff*pg线性化出处理

yg = sdpvar(ngen,Horizon); % ngen 为发电机组数 ,Horizon 为时序性

cons = [cons, yg <= PG, yg >= PG-repmat(Pgmax,1,Horizon).*(1-OnOff), repmat(Pgmin,1,Horizon).*OnOff <= yg <= repmat(Pgmax,1,Horizon).*OnOff];

2 绝对值线性化

对于模型中常用到的绝对值模型，在yalmip里面可以用implies函数轻松解决，下面先分析一下implies函数的用法。

在官网中，implies定义的是逻辑事件间的关系，换言之，implies(A,B)指的就是如果事件A为真，则B为真，即定义的是A -> B的关系。

在实际应用中，也会用到01状态->01状态的映射关系或者01状态->线性约束的映射关系，用官网的简单例子分析：

d = binvar(1);

F = implies(d,A*x <= b);

上述代码即是01状态->线性约束的映射关系程序，先定义01变量d，然后定义约束F为在d==1时满足约束A*x <= b。

通过上面的分析能够看出来，因为在yalmip编程中是不能用if和if-else语句的，implies用来替代常规程序中的if和if-else语句来实现相应约束，这里注意一点，yalmip编程时对于条件为非变量的情况时仍然可以采用if-else语句，但是当条件为变量时就需要采用implies进行编程。

下面分析采用implies进行线性化，举例在电力系统优化时常会用到负荷波动性的目标，通过程序优化减少负荷波动性可以有效降低发电机组出力（启停）频繁变动和区域电网时段性缺电问题，所以优化目标即是abs(等效负荷-平均负荷)，如下图所示。

从图中能看出来，波动性目标为各时段|等效负荷-平均负荷|之和，在等效负荷大于平均负荷时取值为等效负荷-平均负荷，在等效负荷小于平均负荷时取值为平均负荷-等效负荷。具体程序为（程序仅为示例，介绍用法，并不能单独运行，有些变量赋值不全，详情可参见最终全部程序代码）：

%负荷波动性目标

Pt=sdpvar(1,Horizon); %实时负荷

Pave=sdpvar(1,1); %负荷均值

Pdt=sdpvar(1,Horizon); %负荷差值绝对值

Pt=pload - x_P_w - x_P_v + x_P_ch + x_P_dis - sum(yitaph.*x_Ph) + sum(x_Pp); %等效负荷变量

Pave=sum(Pt)/Horizon; %平均负荷

lpt=binvar(2,Horizon); %二进制判断变量

for ii=1:Horizon %至整个整个时序时间段

cons = [cons, sum(lpt(:,ii)) == 1,

implies(lpt(1,ii), [Pt(1,ii)>=Pave, Pdt == Pt(1,ii) - Pave]); %大于平均值

implies(lpt(2,ii), [Pt(1,ii)<=Pave, Pdt == -Pt(1,ii) + Pave])]; %小于平均值

3 平方线性化

平方项的线性化没有办法实现严格线性化，可以通过分段线性化进行近似表达，举一个最简单的例子。

如上图所示，将该模型分成三段，分段线性化即是在定义域内将模型采用分成n段，在每段上采用线性表达的方式，因此，当分段越细化，拟合的精确度就会越高，为了简化分析，按照图中所示分成三段进行分析，可以得到如下的分段函数。

在该分段非线性模型中，可以通过4个连续型变量w和3个01变量z进一步转换，设b为自变量分点，在该模型中分别为0、1、2、3，得到如下转换模型（参考https://www.cnblogs.com/liuxiang2020/p/11254947.html）：

通过上述转化就得到了平方项的线性化转换，同样也能得到转换过程的一般形式如下：

设f(x)函数的分点分别是 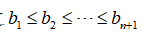，引入n+1个连续变量w和n个0-1变量z，得到下述一般形式模型：

具体程序表达即是将上述模型进行程序语言化，举个例子，在电力系统中，火电机组的成本一般表达为出力的二次函数，表述为y=ax2+bx+c的形式，假定系统含有5个火电机组，可以得到程序表达如下所示（程序仅为示例，介绍用法，并不能单独运行，有些变量赋值不全，详情可参见最终全部程序代码）：

%分段线性化

gn=5;%分段数

gl1=(Pgmax-Pgmin)./gn;%每个机组分段长度

gl2=zeros(3,gn+1);

for i=1:3

gl2(i,:)=Pgmin(i):gl1(i):Pgmax(i);%分点

cons = [cons, x_pf(1,:)==gl2(1,:).^2*gw1];

cons = [cons, x_pf(2,:)==gl2(2,:).^2*gw2];

cons = [cons, x_pf(3,:)==gl2(3,:).^2*gw3];

cons = [cons, gw1(1,:)<=gz1(1,:)];

for i=2:gn

cons = [cons, gw1(i,:)<=gz1(i-1,:)+gz1(i,:)];

cons = [cons, gw1(gn+1,:)<=gz1(gn,:)];

cons = [cons, sum(gz1)==ones(1,Horizon)];

cons = [cons, gw2(1,:)<=gz2(1,:)];

for i=2:gn

cons = [cons, gw2(i,:)<=gz2(i-1,:)+gz2(i,:)];

cons = [cons, gw2(gn+1,:)<=gz2(gn,:)];

cons = [cons, sum(gz2)==ones(1,Horizon)];

cons = [cons, gw3(1,:)<=gz3(1,:)];

for i=2:gn

cons = [cons, gw3(i,:)<=gz3(i-1,:)+gz3(i,:)];

cons = [cons, gw3(gn+1,:)<=gz3(gn,:)];

cons = [cons, sum(gz3)==ones(1,Horizon)];

cons = [cons, PG(1,:)==gl2(1,:)*gw1];

cons = [cons, PG(2,:)==gl2(2,:)*gw2];

cons = [cons, PG(3,:)==gl2(3,:)*gw3];

结语：在编程过程中，需要我们对于模型所遇到的问题进行灵活处理，比较常见的三种线性化方法如本文所述，仍然有些高端线性化的方法通过更加复杂的数学推导可以得到，如两阶段鲁棒优化、二阶锥约束等，以后会陆续更新。

完整电力程序代码： 含风电电力系统低碳调度matlab代码-专业指导文档类资源-CSDN下载 本文参考考虑源荷两侧不确定性的含风电电力系统低碳调度，编写计及源荷两侧不确定性对含风电电力系统低碳调更多下载资源、学习资料请访问CSDN下载频道. https://download.csdn.net/download/zhangxd212489/79381892

电力程序定做可私信。