- 输入网页链接,自动生成快照
- 标签化管理网页链接
|
|
大力的饺子 · 驻槟城总领事鲁世巍在“共建‘一带一路’与马中 ...· 5 月前 · |
|
|
仗义的花生 · 辽宁省改革完善全科医生培养与使用激励机制的实 ...· 6 月前 · |
|
|
朝气蓬勃的仙人掌 · 在 Azure IoT Edge ...· 7 月前 · |
|
|
不拘小节的排球 · MySQL 半同步复制模式说明及配置示例 ...· 1 年前 · |
|
|
私奔的登山鞋 · 生态环境部建设项目环境影响报告书(表)审批程序规定· 1 年前 · |
1.1 KDD2021:盒马-融合反事实预测与MDP模型的清滞销定价算法
本篇想法来源:
因果推断与反事实预测——盒马KDD2021的一篇论文(二十三)
盒马论文提到了
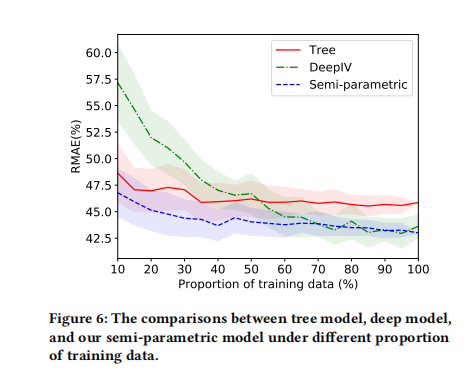
- 论文模型:半参数模型,上图是顺着使用数据的比例增加三个模型的RMAE,
- 对比方案1-XGB:将折扣Treatment作为特征放入模型中预估销量值,但是这个模型本身存在混杂因子,估计是有偏的;
- 对比方案2-DeepIV:将三级品类的平均价格(treatment)作为工具变量,建模深度学习模型刻画折扣和销量的关系,其中折扣Treatment建模成高斯分布
其中主结构模型为:
\mathbb{E}\big[\ln(Y_i/Y_i^\text{nor})\big] =g(d_i;L_i,\theta) + h(d_i^\text{o},x_i) - g(d_i^\text{o};L_i,\theta) E [ ln ( Y i / Y i nor ) ] = g ( d i ; L i , θ ) + h ( d i o , x i ) − g ( d i o ; L i , θ )\mathbb{E}\big[\ln(Y_i/Y_i^\text{nor})\big] =平均折扣销(predict-model)+特殊折扣增量(price-elasticity) E [ ln ( Y i / Y i nor ) ] = 平 均 折 扣 销 ( p r e d i c t − m o d e l ) + 特 殊 折 扣 增 量 ( p r i c e − e l a s t i c i t y )
其中关于盒马那篇文章提到的半参数模型,思路上有一些启发,这里就自己沿着他们的思路DIY一下,借用微软开源的EconML来实现,让我来快速介绍一下本篇会尝试几种思路。
X-协变量Covariates(比如收入);Y-Responses(销量);W-混淆因子;T-干预treatment(比如折扣)
- 实验测试模型1:Tree模型,将T(干预treatment)作为特征直接加到模型里面,也就是此时没有T/W/X,都是自变量,直接使用最简单的XGBoost
- 实验测试模型2:将T作为IV,与盒马一样,借由Econml开源的deepIV
-
实验测试模型3:本篇比较想尝试的,分为两个:
- 无干预样本(T=0):Tree-based模型 D M L − C A T E ( Y ∣ X , W , T ) 这里指的是,利用DML来求在X|W特定情况下,有干预的情况下的异质性处理效应CATE,那么这个CATE代表的是,有干预下的弹性增量
所以这里 : Tree-based模型
盒马的弹性系数问题:
当然盒马那里提出了价格弹性,而且品类非常细分,本篇没那么细致的数据就先不考虑这种方式。
同时价格弹性与笔者这里提到的CATE在log-log DML回归其实是等价的。而且,价格弹性按照盒马论文中,不同分类有不同的价格弹性,那么这里可以非常弹性的根据x/t来进行预测。可能更加符合算法工程上。
后续也会拿价格弹性来试试,不过数据不够,相关如看:
因果推断与反事实预测——利用DML进行价格弹性计算(二十四)另外补充一个问题,就是为什么不直接使用DML中的model_y来直接预测?
model_y训练的时候,只是把T删除,训练集中,不仅有T=0样本,还有T=1的样本。笔者思路没有严格按照 【因果推断/uplift建模】Double Machine Learning(DML) 文章中所描述的那样。
2.1 数据生成
这里很简单粗暴跟着Econml里面的代码来生成数据,只是实验,不太严谨。。
笔者使用的软件版本:
econml.__version__,keras.__version__,xgboost.__version__,tensorflow.__version__ >>> ('0.12.0', '2.6.0', '1.3.3', '2.6.0')数据生成:
import econml ## Ignore warnings import warnings warnings.filterwarnings("ignore") # Main imports from econml.dml import DML, LinearDML, SparseLinearDML, CausalForestDML # Helper imports import numpy as np from itertools import product from sklearn.linear_model import (Lasso, LassoCV, LogisticRegression, LogisticRegressionCV,LinearRegression, MultiTaskElasticNet,MultiTaskElasticNetCV) from sklearn.ensemble import RandomForestRegressor,RandomForestClassifier from sklearn.preprocessing import PolynomialFeatures import matplotlib.pyplot as plt import matplotlib from sklearn.model_selection import train_test_split %matplotlib inline # Treatment effect function def exp_te(x): return np.exp(2 * x[0])# DGP constants np.random.seed(123) n = 2000 n_w = 30 support_size = 4 n_x = 6 # Outcome support support_Y = np.random.choice(range(n_w), size=support_size, replace=False) coefs_Y = np.random.uniform(0, 1, size=support_size) epsilon_sample = lambda n:np.random.uniform(-1, 1, size=n) # Treatment support support_T = support_Y coefs_T = np.random.uniform(0, 1, size=support_size) eta_sample = lambda n: np.random.uniform(-1, 1, size=n) # Generate controls, covariates, treatments and outcomes W = np.random.normal(0, 1, size=(n, n_w)) X = np.random.uniform(0, 1, size=(n, n_x)) # Heterogeneous treatment effects TE = np.array([exp_te(x_i) for x_i in X]) # Define treatment log_odds = np.dot(W[:, support_T], coefs_T) + eta_sample(n) T_sigmoid = 1/(1 + np.exp(-log_odds)) T = np.array([np.random.binomial(1, p) for p in T_sigmoid]) # Define the outcome Y = TE * T + np.dot(W[:, support_Y], coefs_Y) + epsilon_sample(n) # 生成训练数据 Y_train, Y_val, T_train, T_val, X_train, X_val, W_train, W_val = train_test_split(Y, T, X, W, test_size=.2) # Generate test data #X_test = np.array(list(product(np.arange(0, 1, 0.01), repeat=n_x))) W.shape,T.shape,X.shape,Y.shape#,X_test.shape >>> ((2000, 30), (2000), (2000, 6), (2000))这里的混淆因子W有30个维度,T为0/1变量,X为6维特征
2.2 DML模型:有干预下的Y增量
参考的:
因果推断笔记——DML :Double Machine Learning案例学习(十六)这里测试了四款DML模型:
# Default Setting est = LinearDML(model_y=RandomForestRegressor(), model_t=RandomForestRegressor(), random_state=123) est.fit(Y_train, T_train, X=X_train, W=W_train,cache_values = True) #te_pred = est.effect(X_test) print('LinearDML') # fit(Y, T, X=X, W=W, # Polynomial Features for Heterogeneity est1 = SparseLinearDML(model_y=RandomForestRegressor(), model_t=RandomForestRegressor(), featurizer=PolynomialFeatures(degree=3), random_state=123) est1.fit(Y_train, T_train, X=X_train, W=W_train) #te_pred1 = est1.effect(X_test) print('SparseLinearDML') # Polynomial Features with regularization est2 = DML(model_y=RandomForestRegressor(), model_t=RandomForestRegressor(), model_final=Lasso(alpha=0.1, fit_intercept=False), featurizer=PolynomialFeatures(degree=10), random_state=123) est2.fit(Y_train, T_train, X=X_train, W=W_train) #te_pred2 = est2.effect(X_test) print('DML') # CausalForestDML est3 = CausalForestDML(model_y=RandomForestRegressor(), model_t=RandomForestRegressor(), criterion='mse', n_estimators=1000, min_impurity_decrease=0.001, random_state=123) est3.tune(Y_train, T_train, X=X_train, W=W_train) est3.fit(Y_train, T_train, X=X_train, W=W_train) #te_pred3 = est3.effect(X_test) print('CausalForestDML')
LinearDML;SparseLinearDML;DML;CausalForestDML2.3 Tree-based模型
这里干预Tree-based模型,有两个,也就是1.2里面说的,
- 测试模型1,需要W,X,T都作为解释变量;
- 测试模型3,需要W,X作为解释变量且干预=0的样本
import xgboost #import shap import numpy as np #shap.initjs() import numpy as np import pandas as pd from sklearn import preprocessing import lightgbm as lgb from sklearn.metrics import mean_squared_error # 均方误差 from sklearn.metrics import mean_absolute_error # 平方绝对误差 from sklearn.metrics import r2_score # R square # 测试模型3,只筛选T=0的样本 Y_train_2 = np.array([Y_train[n] for n,i in enumerate(T_train) if i ==0 ] ) T_train_2 = np.array([T_train[n] for n,i in enumerate(T_train) if i ==0 ] ) if X_train.shape[1] == 1: X_train_2 = np.array([X_train[n] for n,i in enumerate(T_train) if i ==0 ] ).reshape((-1,1)) else: X_train_2 = np.array([X_train[n] for n,i in enumerate(T_train) if i ==0 ] )#.reshape((-1,1)) W_train_2 = np.array([W_train[n] for n,i in enumerate(T_train) if i ==0 ] )#.reshape((-1,1)) # 训练集 XW_train_0 = np.hstack((X_train_2,W_train_2)) # 测试模型3-只有干预=0的样本 XW_train_0_1 = np.hstack((X_train,W_train)) XWT_train_0_1 = np.hstack((XW_train_0_1,T_train.reshape((-1,1)))) # 测试模型1-W,X,T都作为特征的训练集 # 生成验证集 XW_val = np.hstack((X_val,W_val)) # 测试数据集 XWT_Val = np.hstack((XW_val,T_val.reshape((-1,1)))) # 测试数据集以上就是训练、验证数据的生成过程
然后就是非常简单的训练与预测的过程:
# 测试模型3-只有T=0的情况下 model_0 = xgboost.XGBRegressor().fit(XW_train_0, Y_train_2) # 测试模型1-xwt模型 - 都包括 model_01 = xgboost.XGBRegressor().fit(XWT_train_0_1, Y_train) # 测试模型3-只有T=0的情况下- 验证集预测 y_val_xgb_0 = model_0.predict(XW_val) # 测试模型1- 验证集预测 y_val_xgb_01 = model_01.predict(XWT_Val)2.4 deepIV训练与预测
本篇需参考:因果推断笔记——工具变量、内生性以及DeepIV(六)
deepIV与测试模型1/3不一样,是把T作为IV变量
#T_train.shape,X_train.shape,W_train.shape t_x = 1 + X_train.shape[1] w_x = W_train.shape[1] + X_train.shape[1] print('t+x',t_x) print('w+x',w_x) from econml.iv.nnet import DeepIV import keras import numpy as np import matplotlib.pyplot as plt # 构建模型,需要留意如果W|X维度不一致,需要重新设置,input_shape # w+x treatment_model = keras.Sequential([keras.layers.Dense(128, activation='relu', input_shape=(w_x,)), # input_shape=(2,) keras.layers.Dropout(0.17), keras.layers.Dense(64, activation='relu'), keras.layers.Dropout(0.17), keras.layers.Dense(32, activation='relu'), keras.layers.Dropout(0.17)]) # t+x,如果T|X维度不一致需要重新设置 response_model = keras.Sequential([keras.layers.Dense(128, activation='relu', input_shape=(t_x,)), # input_shape=(2,) keras.layers.Dropout(0.17), keras.layers.Dense(64, activation='relu'), keras.layers.Dropout(0.17), keras.layers.Dense(32, activation='relu'), keras.layers.Dropout(0.17), keras.layers.Dense(1)]) # deepIV模型初始化 keras_fit_options = { "epochs": 100, "validation_split": 0.1} deepIvEst = DeepIV(n_components = 10, # number of gaussians in our mixture density network m = lambda z, x : treatment_model(keras.layers.concatenate([z,x])), # treatment model h = lambda t, x : response_model(keras.layers.concatenate([t,x])), # response model n_samples = 1, # number of samples to use to estimate the response use_upper_bound_loss = False, # whether to use an approximation to the true loss n_gradient_samples = 1, # number of samples to use in second estimate of the response (to make loss estimate unbiased) optimizer='adam', # Keras optimizer to use for training - see https://keras.io/optimizers/ first_stage_options = keras_fit_options, # options for training treatment model second_stage_options = keras_fit_options) # options for training response model # deepiv模型训练 deepIvEst.fit(Y=Y_train,T=T_train,X=X_train,Z=W_train) # deepiv预测 y_val_deepiv_01 = deepIvEst.predict(T_val, X_val)留意treatment_model 、response_model 的Input维度是需要自行调整的
2.5 结果比较
# 测试模型3 有四款模型,四类Y预测值的增量 # 这里 当T=0 直接用预测结果,当T=1的时候,就是y_xgb + y_dml te_pred = est.effect(X_val) te_pred1 = est1.effect(X_val) te_pred2 = est2.effect(X_val) te_pred3 = est3.effect(X_val) model_name = ['LinearDML','SparseLinearDML','DML','CausalForestDML'] print('实验模型1-MSE:',mean_squared_error(Y_val,y_val_xgb_01)) print('实验模型2-deepiv MSE:',mean_squared_error(Y_val,y_val_deepiv_01)) for tn,tp in enumerate([te_pred,te_pred1,te_pred2,te_pred3]): y_val_xgb_0_dml1 = [] for n,t in enumerate(T_val): x = y_val_xgb_0[n] if t == 1: y_val_xgb_0_dml1.append(x+tp[n]) else: y_val_xgb_0_dml1.append(x) print(f'实验模型3 -DML-{model_name[tn]}的MAE:',mean_squared_error(Y_val,y_val_xgb_0_dml1))最后的结果使用MSE
实验模型1-MSE: 0.4982044649307843 实验模型2-deepiv MSE: 5.159633681241892 实验模型3-DML- LinearDML的MSE: 0.5558297771296007 实验模型3-DML- SparseLinearDML的MSE: 1.8249646076083048 实验模型3-DML- DML的MSE: 0.9855352650079277 实验模型3-DML- CausalForestDML的MSE: 0.4753863023209694这里也仅是实验,不过可以看到,
实验模型1效果还行;
实验模型2,deepIV好像MSE很高,可能是我哪里写错了;
实验模型3,DML,这里随着不同的DML方法波动挺大,这里看到CausalForestDML结果优于实验模型12.6 随着X维度上升,各模型的准确性
以上是X为6维的时候的结果,我们来对比一下X维度提升最终结果的情况:
# x=1维 实验模型1-MSE: 0.5160967348769703 实验模型2-deepiv MSE: 35.59973032150524 实验模型3-DML- LinearDML的MSE: 0.5813808010457113 实验模型3-DML- SparseLinearDML的MSE: 0.5019110708791529 实验模型3-DML- DML的MSE: 0.9961407722015089 实验模型3-DML- CausalForestDML的MSE: 0.5089520789034898 # x=3维度 实验模型1-MSE: 0.5449129530089527 实验模型2-deepiv MSE: 22.62998950191628 实验模型3-DML- LinearDML的MSE: 0.5069041205691804 实验模型3-DML- SparseLinearDML的MSE: 0.5152944232346934 实验模型3-DML- DML的MSE: 1.031471234778512 实验模型3-DML- CausalForestDML的MSE: 0.4678926411195991 # x=6维度 实验模型1-MSE: 0.4982044649307843 实验模型2-deepiv MSE: 5.159633681241892 实验模型3-DML- LinearDML的MSE: 0.5558297771296007 实验模型3-DML- SparseLinearDML的MSE: 1.8249646076083048 实验模型3-DML- DML的MSE: 0.9855352650079277 实验模型3-DML- CausalForestDML的MSE: 0.4753863023209694 # x=9维度 实验模型1-MSE: 0.5646551531847374 实验模型2-deepiv MSE: 3.2337960384156053 实验模型3-DML- LinearDML的MSE: 0.6796584984496488 实验模型3-DML- SparseLinearDML的MSE: 10.997935994944733 实验模型3-DML- DML的MSE: 0.864753230235102 实验模型3-DML- CausalForestDML的MSE: 0.5614196162924773根据上述结果画一个非常简单的图:
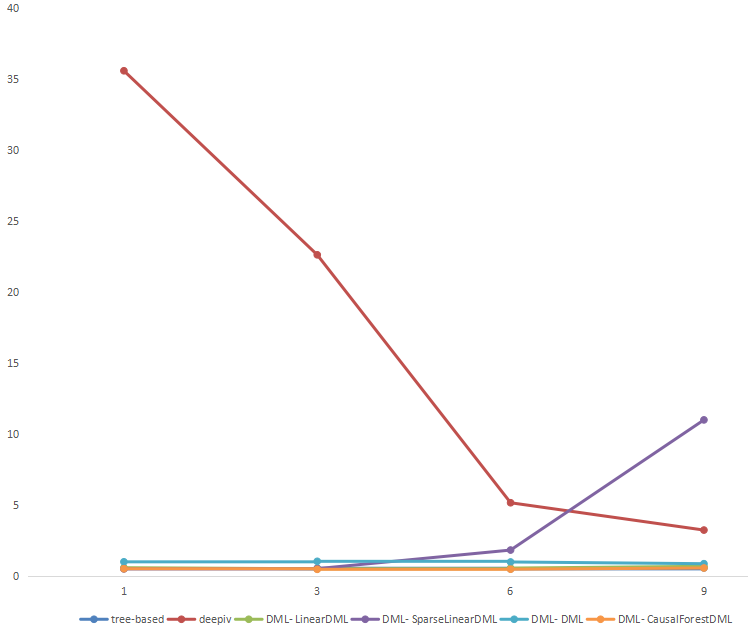
可以看到deepiv随着特征增加,下降非常快,所以DNN对高纬度的处理还是很给力的;
tree-based的模型1,其实非常稳定;
DML里面CausalForestDML效果一直比较好回看盒马那篇论文:
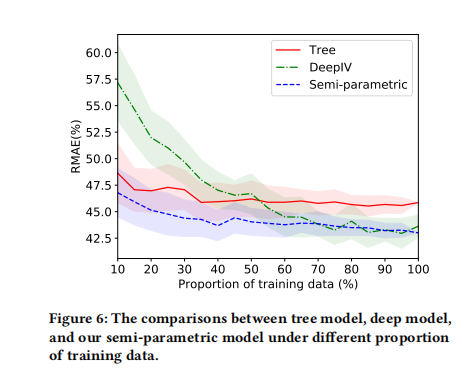
也可以看到deepIV模型的潜力,数据量较小,loss非常大,随着数据新增模型的效果也是在一直提升的。
所以,整体来看,deepIV在较为复杂的数据、数据量较大的情况下,不外乎是一个值得考虑的模型2.7 短期小结
这里实验模型3是比较想看到效果,几个模型都没有任何调参,所以“自然”情况下的对比来看,模型3反事实预测的效果还是可以有的;
BUT,实验模型1,把Treatment作为特征,虽然估计有偏,不够严谨,但未尝不是一个好方式,当然适用性方面,如果X|W维度很高,感觉模型实验1可能也会有大问题未完待续… 欢迎拍砖
文章目录1 导言1.1 KDD2021:盒马-融合反事实预测与MDP模型的清滞销定价算法1.2 本篇想法2 代码2.1 数据生成2.2 DML模型:有干预下的Y增量2.3 Tree-based模型2.4 deepIV训练与预测2.5 结果比较2.6 短期小结1 导言1.1 KDD2021:盒马-融合反事实预测与MDP模型的清滞销定价算法本篇想法来源:因果推断与反事实预测——盒马KDD2021的一篇论文(二十三)盒马论文提到了论文模型:半参数模型,上图是顺着使用数据的比例增加三个模型的RMAE,Deep Learning Part IV 深度学习(Deep Learning) 中文版 [ 感谢大神们的翻译 Github 地址:https://github.com/exacity/deeplearningbook-chinese ],中文文字版,【 在线版本地址:https://exacity.github.io/deeplearningbook-chinese/ 】 深度学习(Deep Learning) 英文版,英文扫描版【在线地址:http://www.deeplearningbook.org/】; Deep Learning with Python 2017_w ,英文文字版; 由于我的最大上传权限是 60 MB ,而且 英文版的 Deep Leraning 文件太大,所以把它们压缩成了 5 个分卷【每个分卷消耗 1 个资源分】EconML:用于基于ML的异构处理效果估计的Python包 EconML是一个Python软件包,用于通过机器学习从观察数据中估计异构处理效果。 此软件包是作为Microsoft Research的一部分设计和构建的,目的是将最新的机器学习技术与计量经济学相结合,以使自动化解决复杂的因果推理问题。 EconML的承诺: 在计量经济学和机器学习的交集中实现文献中的最新技术 保持建模效果异质性的灵活性(通过诸如随机森林,增强,套索和神经网络之类的技术),同时保留对所学模型的因果解释,并经常提供有效的置信区间 使用统一的API 建立在用于机器学习和数据分析的标准Python软件包的基础上 机器学习的最大希望之一就是在众多领域中自动化决策。 许多数据驱动的个性化决策方案的核心是对异构处理效果的估计:对于具有特定特征集的样本,干预对感兴趣结果的因果关系是什么? 简而言之,该工具包旨在测量某些治疗变量T对结果变量Y的因果效应,控制一组特征X, W以及该效应如何随X 。 所实施的方法甚至适用于观测(非实验或历史)数据集。 为了使估计结果具有因果关系,有些方法假定没有观察到的混杂因素(即, X,微软EconML简介:基于机器学习的Heterogeneous Treatment Effects估计 机器学习最大的promise之一是在许多领域实现决策的自动化。 许多数据驱动的决策场景的核心问题是对heterogeneous treatment effects的估计,也即:对于具有特定特征集的样本,干预对输出结果的causal effect是什么? 简言之,这个Python工具包旨在: 测量某些干预变量T对结果变量Y的causal effect 控制一组特征X和W,来衡量causal effect如文章目录1 理论介绍1.1 Instrumental variable解释1.2 因果推断中:内生性的一个有意思的例子1.2 与代理变量(proxy variable)的对比1.3 连玉君老师的简易解读2 econML实现 DeepIV 同系列可参考: 因果推断笔记——因果图建模之微软开源的dowhy(一) 因果推断笔记—— 相关理论:Rubin Potential、Pearl、倾向性得分、与机器学习异同(二) 因果推断笔记——python 倾向性匹配PSM实现示例(三) 因果推断笔记——双重差分理论、假文章目录1 导言1.1 价格需求弹性介绍1.2 由盒马反事实预测论文开始1.3 DML - 价格弹性预测推理步骤2 案例详解2.1 数据清理2.2 [v1版]求解价格弹性:OLS回归2.3 [v2版]求解价格弹性:Poisson回归+多元岭回归2.4 [v3版]求解价格弹性:DML2.4.1 DML数据准备 + 建模 + 求残差2.4.2 三块模型对比2.4.3 稳健性评估 1.1 价格需求弹性介绍 经济学课程里谈到价格需求弹性,描述需求数量随商品价格的变动而变化的弹性。价格一般不直接影响需求,DDL、DML和DCL的区别与理解 数据操纵语言。它们是SELECT、UPDATE、INSERT、DELETE,就像它的名字一样,这4条命令是用来对数据库里的数据进行操作的语言。 数据定义语言。DDL比DML要多,主要的命令有CREATE、ALTER、DROP等,DDL主要是用在定义或改变表(TABLE)的结构,数据类型,表之间的链接和约束等初始化工作上,他们大多在建立表时使用。删除客户“刘一鸣”。 执行 SQL 代码“delete from customer where cName=’ 刘一鸣 ‘”,会出现删除异常。 打开从表 orders 的设计视图,单击“外键”,出现 orders 表外键编辑窗口,下拉选中“删除时”的状态值为“SET NULL”。 如果删除客户时,该客户所下订单亦跟着全部删除,则下拉选中“删除时”的状态值为“CASCADE”。 >>知识点【第3章 DDL 和 DML】 作者:明金同学Machines are increasingly doing “intelligent” things: Facebook recognizes faces in photos, Siri understands voices, and Google translates websites. The fundamental insight behind these breakthroughs is as much statistical as computational.上午4:00 - 7:00 AM 2021年8月15日 2021 年 8 月 14 日下午 4:00 - 晚上 7:00 时间 2021 年 8 月 14 日下午 1:00 - 4:00 实时缩放链接 在会议期间在 KDD 21 虚拟平台内共享。 近年来,无论是学术研究还是行业应用,都越来越多地使用机器学习方法来衡量细粒度的因果效应,并根据这些因果估计设计最佳策略。 和等开源软件包为应用研究人员和行业从业者提供了一个统一的接口,使用各种机器学习方法进行因果推理。 本教程将涵盖的主题包括元学习器的条件处理效果估计器和基于树的算法、模型验证和敏感性分析、优化算法(包括策略精简和成本优化)。 此外,本教程将演示这些算法在行业用例中的生成。文章目录1 因果推断与线性回归的关系1.1 DML的启发1.2 特殊的离散回归 = 因果?2 因果推断中的ITE 与SHAP值理论的思考 1 因果推断与线性回归的关系 第一个问题也是从知乎的这个问题开始: 因果推断(causal inference)是回归(regression)问题的一种特例吗? 其中经济学大佬慧航提到过,回归只是工具,因果推断可以用,其他研究方向也可以用。 在此给出我的看法, 因果推断,是需要考虑干预得(Y|X,T),其中干预效应是主要的差异点; 而一般的多元,只是(Y|X),并DoWhy | An end-to-end library for causal inference Getting started with DoWhy: A simple example 使用因果推理的四个步骤来动手估计因果效应:建模model、识别identify、估计 estimate 和反驳 refute。 因果关系定义 假设我们想要找到采取行动A对结果y的因果影响,要定义因果影响,考虑两个世界: 世界1(真实世界): 行动A被采取,观察到Y 世界2(反事实世界): 没有采取行动A,但其他一以下是用econml包写的python代码,用于计算处理效应异质性:from econml.dml import LinearDML import econml.dml import matplotlib.pyplot as plt# 定义因果树模型 model = LinearDML(cost_function='heteroskedastic')# 训练模型 model.fit(X_train, y_train, treatment_train, W_train=None, estimand='ATE')# 获取处理效应异质性结果 heteroskedastic_effect = model.effect(X_test, W_test=None)# 可视化结果 plt.scatter(heteroskedastic_effect.index, heteroskedastic_effect) plt.xlabel('Index') plt.ylabel('Heteroskedastic Effect') plt.show()
|
|
私奔的登山鞋 · 生态环境部建设项目环境影响报告书(表)审批程序规定 1 年前 |